Критерий согласия. Составной критерий и облость его применения.
Для проверки соответствия эмпирического распределения теоретическому (гипотезы) можно наложить на гистограмму теоретическую кривую (рис. 6).
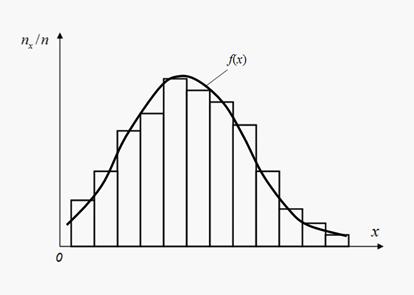Рис.
6. Гистограмма и теоретическая плотность
распределения
При
этом неизбежно обнаружатся расхождения,
либо случайные, связанные с ограниченным
объемом наблюдений, либо свидетельствующие
о неправильном подборе выравнивающей
функции (гипотезы). Для ответа на этот
вопрос используют так называемые
«критерии
согласия».
Для этого вводится случайная величина U,
характеризующая расхождение эмпирического
и теоретического распределений в
предположении истинности теоретического
распределения. Мера расхождения U выбирается
таким образом, чтобы функция ее
распределения 
не
зависела от вида выравниваемого
(эмпирического) распределения и достаточно
быстро сходилась по числу наблюдений n к
предельной функции 
.
Затем определяется фактическая степень
расхождения u и
оценивается вероятность 
Малая
величина 
говорит
о том, что полученное расхождение u в
силу чисто случайных причин маловероятно,
и теоретическое распределение плохо
согласуется с эмпирическим. Однако,
большие вероятности не могут считаться
исчерпывающим доказательством истинности
теоретического закона распределения
и свидетельствуют лишь об отсутствии
оснований его отвергнуть.
Иногда
поступают иначе: заранее рассчитывают
меру расхождения 
,
которая может быть превышена с указанной
малой вероятностью, и при 
рассматриваемое
теоретическое распределение отвергают.
Существует
множество критериев согласия, среди
которых наиболее употребительными
являются критерий
Пирсона и критерий
Колмогорова-Смирнова.
В критерии согласия Пирсона мерой расхождения теоретического и эмпирического распределений является взвешенная сумма квадратов отклонений
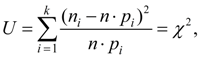(27)
где k –
число интервалов разбиения значений
случайной величины, 
–
количество наблюдений, попавшее в i-й
интервал, 
–
теоретическая вероятность появления
значения из i-го
интервала, n –
общее число наблюдений.
В практических задачах рекомендуется иметь в каждом интервале разбиения не менее 5-10 наблюдений [3].
Обозначим
через t число
независимых связей, наложенных на
вероятности
.
Их общее число равно количеству
характеристик теоретического
распределения, подбираемых по опытным
данным, плюс единица (условие нормировки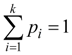 
).
Таким образом, схема применения
критерия
к
оценке согласованности теоретического
и эмпирического распределений сводится
к следующему:
1) Определяется мера расхождения по формуле (27). 2) Определяется число степеней свободы r = k – t. 3) По r и с помощью специальной таблицы [3] определяется вероятность того, что величина, имеющая распределение с rстепенями свободы, превзойдет данное значение . Если эта вероятность весьма мала, гипотеза (теоретическая кривая) отбрасывается как неправдоподобная. Если же эта вероятность относительно велика, гипотезу можно признать не противоречащей полученным экспериментальным данным.
Насколько мала должна быть вероятность р для того, чтобы отбросить или пересмотреть гипотезу, не решается на основе математических соображений и выкладок. На практике, если оказывается, что р < 0.1, рекомендуется проверить или повторить эксперимент. Если заметные расхождения появятся снова, следует искать другой, более подходящий для описания опытных данных закон распределения. Если же вероятность p > 0.1 (относительно велика), то это еще не может считаться доказательством справедливости гипотезы, а говорит лишь о том, что гипотеза не противоречит экспериментальным данным.
В критерии
Колмогорова-Смирнова мерой
расхождения теоретического F(x)
и эмпирического 
распределений
является максимальный модуль разности
(28)
А.Н.Колмогоров
доказал, что при 
независимо
от вида F(x)
вероятность неравенства
(29)
стремится к пределу
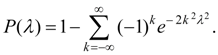(30)
Для
проверки гипотезы по критерию согласия
Колмогорова-Смирнова необходимо
построить функции распределения F(x)
для теоретического и
для
эмпирического распределений, определить
максимум d модуля
разности между ними и найти
.
После этого следует найти по специальной
таблице [2] вероятность
:
|
|
|
|
|
|
0.0 |
1.000 |
0.7 |
0.711 |
1.4 |
0.040 |
0.1 |
1.000 |
0.8 |
0.544 |
1.5 |
0.022 |
0.2 |
1.000 |
0.9 |
0.393 |
1.6 |
0.012 |
0.3 |
1.000 |
1.0 |
0.270 |
1.7 |
0.006 |
0.4 |
0.997 |
1.1 |
0.178 |
1.8 |
0.003 |
0.5 |
0.964 |
1.2 |
0.112 |
1.9 |
0.002 |
0.6 |
0.864 |
1.3 |
0.068 |
2.0 |
0.001 |
Малая вероятность свидетельствует о неприемлемости теоретической функции.