Проверка на нормальность закона распределения вероятности результата измерения с помощью гистограмм.
Функция влияния – это зависимость изменения метрологических характеристик средств измерения от изменения влияющего фактора или от изменения совокупности влияющих факторов.
Гистограмма (в фотографии) — это график распределения полутонов изображения, в котором по горизонтальной оси представлена яркость, а по вертикали — относительное число пикселов с данным значением яркости.
Изучив гистограмму, можно получить общее представление о правильности экспозиции, контрасте и цветовом насыщении снимка, оценить требуемую коррекцию как при съёмке (изменение экспозиции, цветового баланса, освещения либо композиции снимка), так и при последующей обработке.
Критерий согласия Пирсона (х2 – хи-квадрат). Гипотеза о соответствии или несоответствии эмпирического закона распределения вероятности. Алгоритм проверки на нормальность закона распределения.
Критерий Пирсона — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.
Статистика критерия, Для проверки критерия вводится статистика:
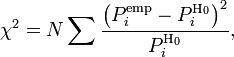где
—
предполагаемая вероятность попадания
в
-й
интервал,
—
соответствующее эмпирическое значение,
—
число элементов выборки из
-го
интервала,
—
полный объём выборки. Также используется
расчет критерия по частоте, тогда:
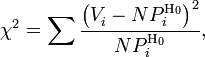где
—
частота попадания значений в интервал.
Эта величина, в свою очередь, является
случайной
(в силу случайности
)
и должна подчиняться распределению
.
Ошибки перго рода. Ошибка второго рода. Вероятность этих ошибок при проверке на нормальность закона распределения. Графики плотности распределения вероятности (хи-квадрат).
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т. е. могут быть допущены ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Вероятность
совершить ошибку первого рода принято
обозначать через 
;
ее называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0.05 или 0.01. Если, например, принят
уровень значимости, равный 0.05, то это
означает, что в пяти случаях из ста мы
рискуем допустить ошибку первого рода
(отвергнуть правильную гипотезу).
Надежность эргономической системы, в которую входят человек, окружающая среда, объект измерений и средство измерений, не безгранична. В ней могут происходить сбои, отказы аппаратуры, скачки напряжения в сети питания, сейсмические сотрясения, отвлечение внимания оператора, описки в записях и многое другое, не имеющее отношения к измерениям. В результате появляются ошибки , вероятность которых, как следует из теории надежности больших систем, не так уж мала. При однократном измерении ошибка может быть обнаружена только путем логического анализа или сопоставления результата с априорным представлением о нем. Установив и устранив причину ошибки, измерение можно повторить. При многократном изменении одной и той же величины постоянного размера ошибки проявляются в том, что результаты отдельных измерений заметно отличаются от остальных. Иногда это отличие настолько большое, что ошибка очевидна. Остается понять и устранить ее причину или просто отбросить этот результат как заведомо неверный. Если отличие незначительное, то это может быть следствием, как ошибки, так и рассеяния отсчета, а, следовательно, показания и результата измерения, которые, согласно основному постулату метрологии, являются случайными. Нужно поэтому иметь какое-то правило, руководствуясь которым принимать решения в сомнительных случаях. После того, как все влияющие факторы учтены, и все поправки в показания внесены, рассеяние результатов при многократном измерении одной и той же физической величины постоянного размера нередко бывает следствием множества причин, вклад каждой из которых незначителен по сравнению с суммарным действием всех остальных. Центральная предельная теорема теории вероятностей утверждает, что результат измерения при этом подчиняется так называемому нормальному закону: кривые плотности распределения вероятности которого при различных значениях дисперсии показаны на рис. 15.
Рис.15. Графики плотности распределения вероятности отсчета при различных дисперсиях.