Среднее арифметическое значение рузультата измерения. Математическое ожидание среднего арифметического. Задача оценки среднего значения и метод ее решения.
Для нормального распределения, а если поступиться эффективностью оценки, то и для всех симметричных распределений, в качестве оценки математического ожидания ряда равноточных наблюдений принимают среднее арифметическое ряда наблюдений.
При п→∞, если отсутствует систематическая погрешность, Q→Qист. Разность vi=Qi— представляет собой случайную погрешность при i-м наблюдении. Она может быть положительной и отрицательной.
Среднее
арифметическое независимо от закона
распределения обладает свойствами: в
качестве оценки дисперсии берется
дисперсия отклонения результата
наблюдения. Средняя квадратическая
погрешность результатов единичных
измерений в ряду измерений. Оценка S рассеяния
единичных результатов измерений одной
и той же физической величины около
среднего их значения, вычисляемая по
формуле: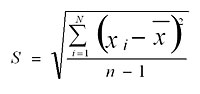
где
хi– результат i-го единичного измерения;
- среднее арифметическое значение измеряемой величины из n единичных результатов.
Математическое
ожидание — среднее
значение случайной
величины, распределение вероятностей
случайной величины, рассматривается
в теории
вероятностей. Обозначается через 
.
В статистике часто используют
обозначение 
.
Д
ля
уяснения физического смысла и ряда
особенностей алгоритмов адаптации мы
начнем с простейшей задачи — оценки
среднего значения случайного процесса
(5.1) где 
—
неизвестная постоянная, а 
—
помеха с нулевым средним значением и
конечной дисперсией. Такая задача
возникает, например, при обработке
результатов измерений или при выделении
постоянного сигнала на фоне шумов.
Наблюдаемая величина
—
это реализация, которую только мы и
можем измерять или обрабатывать.
Е
сли
ошибки, вызываемые помехой, равновероятны,
то наилучшей оценкой после 
наблюдений
будет среднее арифметическое (5.2)
П
одставляя
сюда 
из
(5.1), получим (5.3)
Отсюда
следует, что с ростом числа наблюдений
влияние помех уменьшается, и
оценка 
стремится
к искомому значению
.Преобразуем
теперь оценку (5.2):
(5.5)
Соотношение
(5.5) показывает, что с ростом
влияние
новой информации 
падает,
поскольку вес ее, равный 
,
обратно пропорционален числу измерений,
и при этом
стремится
к
.
Этот факт часто подтверждается и в
жизни: мы должны основывать наши решения
на прошлом опыте, не придавая слишком
большого веса новой информации, которая
сама по себе может вызвать лишь шарахания
из стороны в сторону. Формулы вида (5.5)
издавна использовались при юстировке
точных приборов или при пристрелке во
время стрельбы в форме правила:
-я
поправка берется равной
от
величины полного отклонения.
Точечная оценка дисперсии результата измерения. Стандартное отклонение. Метод максимального правдоподобия как универсальный метод отыскания эффективных оценок числовых характеристик.
Дисперсия -в статистике очень важный показатель, который активно используется в др. видах статистического анализа (проверка гипотез, анализ причинно-следственных связей и др.). Как и среднее линейное отклонение, дисперсия также отражает меру разброса данных вокруг средней величины.
Формула
для расчета дисперсии:
,
D– дисперсия, x– анализируемый
показатель, с черточкой сверху – среднее
значение показателя, n– количество
значений в анализируемой совокупности
данных.
Дисперсия - это средний квадрат отклонений => вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, нужно просто рассчитать среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Разгадка магического слова «дисперсия» заключается всего в трех словах.
Однако в чистом виде, средняя арифметическая, или индекс, дисперсия не используется. Это скорее вспомогательный и промежуточный показатель, который используется для других видов статистического анализа (нет единицы измерения). Из формулы, это квадрат единицы измерения исходных данных.
Стандартное
отклонение
-что бы использовать результат расчета
для более приземленных целей, из нее
извлекают квадратный корень. Получается
- стандартное
отклонение.
В статистике этот показатель еще называют
среднеквадратическим отклонением, но
первое название более короткое и
распространенное. Будем им пользоваться.
Формула стандартного отклонения имеет
вид:
Кстати, стандартное отклонение еще называют сигмой – от греческой буквы, которой его обозначают. Отсюда и название известного статистического метода «6-сигма». То есть 6 стандартных отклонений. Почему 6, расскажу в другой раз.
Стандартное отклонение, очевидно, также характеризует меру рассеяния данных, но теперь (в отличие от дисперсии) его можно сравнивать с исходными данными, так как единицы измерения у них одинаковые (это явствует из формулы расчета). Но и этот показатель в чистом виде не очень информативен, так как в нем заложено слишком много промежуточных расчетов, которые сбивают с толку (отклонение, в квадрат, сумма, среднее, корень). Тем не менее, со стандартным отклонением уже можно работать непосредственно, потому что свойства данного показателя хорошо изучены и известны. К примеру, есть такое правило трех сигм, которое гласит, что в данных с нормальным распределением 997 значений из 1000 будут находиться не далее, чем 3 сигмы в ту или иную сторону от среднего значения. Сигма, как мера неопределенности, также участвует во многих статистических расчетах. С ее помощью устанавливают степень точности различных оценок и прогнозов. Если вариация очень большая, то стандартное отклонение тоже получится большим, следовательно, и прогноз будет неточным, что выразится, к примеру, в очень широких доверительных интервалах.
13.
-----