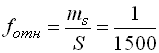9. Однократное измерение (роль априорной информации и пять ее вариантов).

Необходимым условием проведения однократного измерения служит наличие априорной информации. К ней относится, например, информация о виде закона распределения вероятности показания и мере ее рассеяния, которая извлекается из опыта предшествующих измерений. Без априорной информации выполнение однократного измерения бессмысленно. Предварительно проводится тщательный анализ априорной информации. В ходе этого анализа уясняется физическая сущность изучаемого явления, уточняется его модель, определяются влияющие факторы. Априори знание, полученное до опыта и независимо от него (знание априори, априорное знание), т.е. знание, как бы заранее известное

Необходимым условием проведения однократного измерения является наличие априорной информации. К априорной относятся:

1. информация о виде закона распределения вероятно­сти показания и мере его рассеяния, которая извлекается из опыта предшествующих измерений;

2. информация о том, насколько значение измеряемой величины может отличаться от результата однократного измерения, которая может быть представлена классом точ­ности прибора;

3. информация о значении аддитивной и мультиплика­тивной поправки 9_i. Если значение поправки не известно,то оно учитывается ситуационной моделью, согласно кото­рой значение поправки может быть любым с одинаковой вероятностью в пределах от 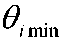до .

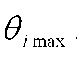10. Многократное измерениес равноточными значениями отсчета (дисперсия, равноточные и неравноточные значения отсчета).

Дисперсия случайной величины — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается   в русской литературе и  (англ. variance) в зарубежной. В статистике часто употребляется обозначение   или  . Квадратный корень из дисперсии, равный  , называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

Из неравенства Чебышева следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75 % случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89 % — не более чем на три.

11. Точечные оценки числовых характеристик (определение точечности; требования к оценкам: состоятельность, несмещенность, эффективность).

Под точностью измерений понимается степень близости результата измерения к истинному значению измеряемой величины. Точность результата измерений зависит от условий измерений.

Для равноточных результатов измерений мерой точности является средняя квадратическая ошибка m, определяемая по формуле Гаусса:

 .

Средняя квадратическая ошибка обладает устойчивостью при небольшом числе измерений.

Предельная ошибка.

Вследствие третьего свойства случайные ошибки, превышающие по абсолютной величине значение 2m, встречаются редко (5 на 100 измерений). Еще реже погрешности больше 3m (3 из 1000 измерений). Поэтому устроенную погрешность называют предельной ошибкой

Для особо точных измерений в качестве предельной ошибки принимают

Все вышеперечисленные ошибки называют абсолютными. В геодезии в качестве специальных характеристик точности измерений используется относительная ошибка – отношение абсолютной ошибки к среднему значению измеряемой величины, которое выражается в виде простой дроби с единицей в числителе, например