Вопрос 1
Ко́мпле́ксные
чи́сла (устар.
Мнимые
числа), —
расширение поля вещественных чисел,
обычно обозначается
.
Любое комплексное число может быть
представлено как формальная сумма
,
где
и
—
вещественные числа,
—
мнимая единица
Алгебраическая форма
Запись
комплексного числа
в
виде
,
,
называется алгебраической
формой
комплексного числа.
Сумма
и произведение комплексных чисел могут
быть вычислены непосредственным
суммированием и перемножением таких
выражений, как обычно раскрывая скобки
и приводя подобные, чтобы представить
результат тоже в стандартной форме (при
этом надо учесть, что
):
Тригонометрическая и показательная формы
Если
вещественную
и
мнимую
части
комплексного числа выразить через
модуль
и
аргумент
(
,
),
то всякое комплексное число
,
кроме нуля, можно записать в
тригонометрической
форме
Действия над комплексными числами
Сравнение
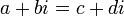означает,
что
и
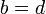(два
комплексных числа равны между собой
тогда и только тогда, когда равны их
действительные и мнимые части).
Сложение
Вычитание
Умножение
Деление
Вопрос 2
Формула Муавра имеет вид:
где
—
модуль, а
—
аргумент комплексного числа. В современной
символике она опубликована Эйлером
в 1722
году.
Приведенная формуле справедлива при
любом целом n,
не обязательно положительном.
Аналогичная
формула применима также и при вычислении
корней
-ой
степени из ненулевого комплексного
числа:
Вопрос 3
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексныхчисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы
В том случае, когда количество строк матрицы равняется количеству ее столбцов, матрица называется квадратной/
Матрица, которая содержит только одну строчку или один столбец называется вектором.
Квадратная матрица, у которой в главной диагонали стоят ненулевые элементы, а все остальные - это нули называется диагональная матрица.
Если все элементы матрицы нули, то это нулевая матрица.
Если в данной матрице поменять строки и столбцы местами, то получится транспонированная матрица данной.
Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.
Умножение матрицы на число
Умножение
матрицы 
на
число 
(обозначение: 
)
заключается в построении матрицы 
,
элементы которой получены путём умножения
каждого элемента матрицы
на
это число, то есть каждый элемент
матрицы
равен
Сложение матриц
Сложение
матриц 
есть
операция нахождения матрицы 
,
все элементы которой равны попарной
сумме всех соответствующих элементов
матриц
и
,
то есть каждый элемент матрицы
равен
Умножение матриц
Умножение
матриц (обозначение: 
,
реже со знаком умножения 
) —
есть операция вычисления матрицы
,
каждый элемент которой равен сумме
произведений элементов в соответствующей
строке первого множителя и столбце
второго.
Умножение вектора на матрицу
По обычным правилам матричного умножения осуществляется умножение на матрицу слева вектора-столбца, а также умножение вектора-строки на матрицу справа. Поскольку элементы вектора-столбца или вектора-строки можно записать (что обычно и делается), используя один, а не два индекса, это умножение можно записать так:
для вектора-столбца v (получая новый вектор-столбец Av):
Комплексное сопряжение
Если
элементами матрицы 
являются
комплексные числа, то комплексно
сопряжённая (не
путать с эрмитово
сопряжённой!
см. далее) матрица равна 
.
Здесь 
—
число, комплексно
сопряжённое к 
.
Транспонирование и эрмитово сопряжение
Транспонирование
уже обсуждалось выше: если
,
то 
.
Для комплексных матриц более
употребительно эрмитово
сопряжение: 
.
С точки зрения операторного взгляда на
матрицы, транспонированная и эрмитово
сопряжённая матрица — это матрицы
оператора, сопряжённого относительно скалярногоили эрмитова произведения,
соответственно.