Непрерывные случайные величины
Пусть
– непрерывная случайная величина,
которая в результате
испытаний приняла значение
.
Допустим, что вид плотности распределения
функции
задан, но неизвестен параметр
,
которым определяется эта функция.
О.2.3. Функцией правдоподобия непрерывной случайной величины называется функция аргумента , имеющая вид:
,
где – фиксированные числа.
Оценку максимального правдоподобия неизвестного параметра распределения непрерывной случайной величины ищут так же, как в случае дискретной случайной величины.
Пример
2.
Найти методом максимального правдоподобия
оценку параметра
показательного распределения
,
если в результате
испытаний случайная величина
,
распределенная по показательному
закону, приняла значения
.
Решение
Составим
функцию правдоподобия
,
учитывая, что
:
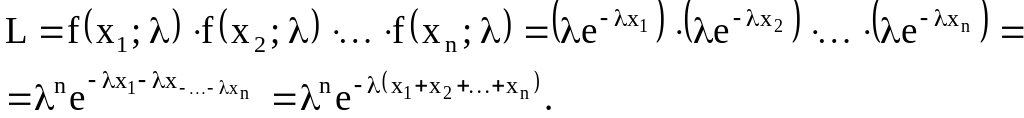
Отсюда
.
Найдем логарифмическую функцию правдоподобия:
.
Таким образом,
Найдем точку максимума функции .
1. Найдем первую производную по :
.
2. Составим уравнение правдоподобия:
.
Найдем критическую точку, решив уравнение правдоподобия относительно :
.
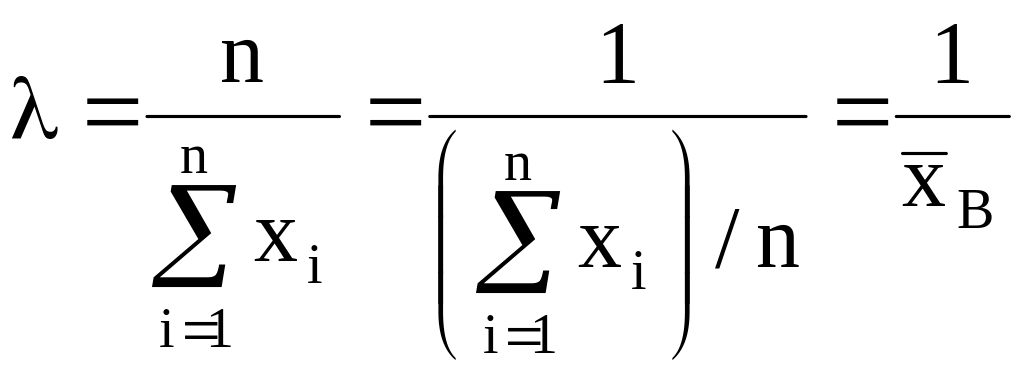Таким
образом,
– критическая точка.
3. Найдем вторую производную по :
.
Очевидно,
что при
вторая производная
:
.
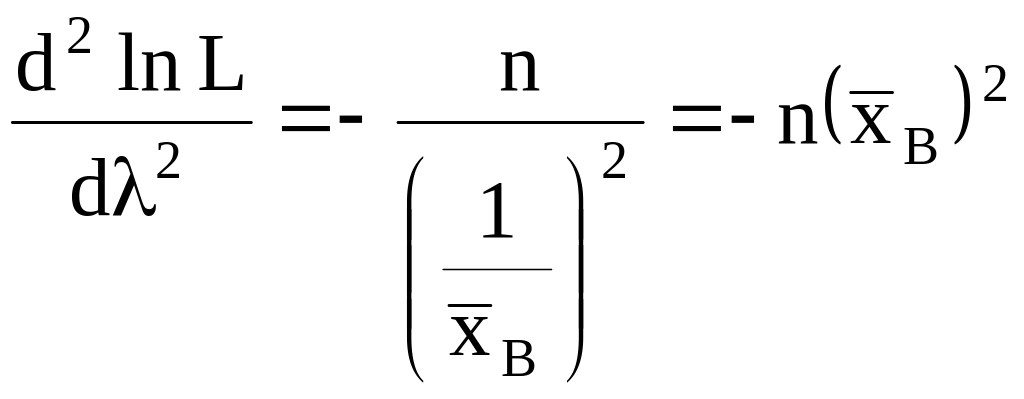Следовательно, – точка максимума и, значит, в качестве оценки максимального правдоподобия параметра показательного распределения надо принять величину, обратную выборочной средней: .
Замечание
Если
плотность распределения
непрерывной случайной величины
определяется двумя неизвестными
параметрами
и
,
то функция правдоподобия
является функцией двух независимых
аргументов
и
,
т.е.
где – наблюдавшиеся значения величины .
Далее находят логарифмическую функцию правдоподобия и для отыскания ее максимума составляют и решают систему:
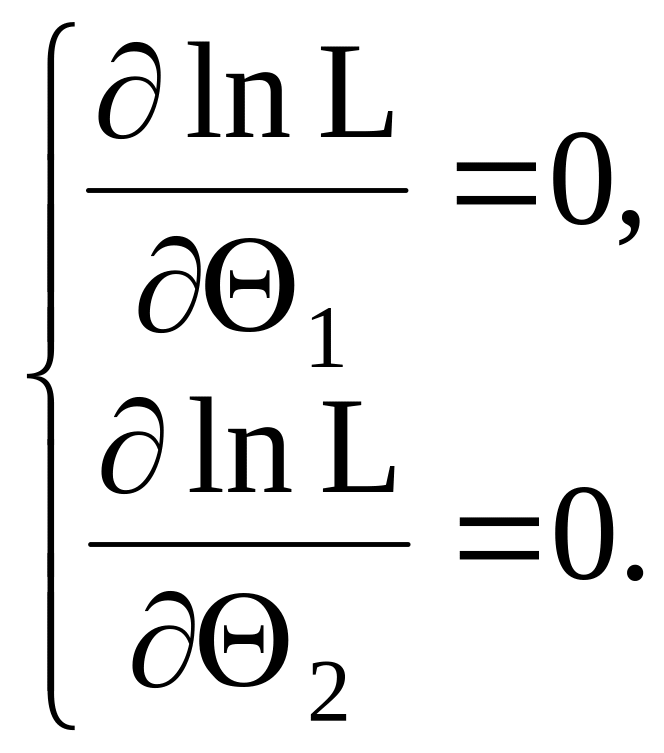
Метод максимального правдоподобия имеет ряд достоинств:
1. Оценки максимального правдоподобия, вообще говоря, состоятельны (но они могут быть смещенными), распределены асимптотически нормально (при больших значениях и приближенно нормальны) и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками.
2. Если для оцениваемого параметра существует эффективная оценка , то уравнение правдоподобия имеет единственное решение .
3. Этот метод наиболее полно использует данные выборки об оцениваемом параметре, поэтому он особенно полезен в случае малых выборок.
Основным недостатком метода максимального правдоподобия является трудность вычисления оценок, связанных с решением уравнений правдоподобия, чаще всего нелинейных. Существенно так же и то, что для построения оценок максимального правдоподобия и обеспечения их «хороших» свойств необходимо точное значение типа анализируемого закона распределения, что во многих случаях оказывается практически нереальным.