ЛЕКЦИЯ №

Статистические методы обработки экспериментальных данных

1. Обработка результатов наблюдений по методу наименьших квадратов.

2. Принцип максимального правдоподобия.

Введение

Довольно часто в практике исследовательской работы встречаются ситуации, когда при изучении тех или иных случайных величин и обработке статистического материала, полученного в результате эксперимента, характер закона распределения изучаемых случайных величин известен до опыта, исходя из теоретических или физических соображений, связанных с существом решаемой задачи. Например, часто можно заранее утверждать, что случайная величина подчинена нормальному закону распределения. Тогда возникает задача определения некоторых параметров распределения на основе опытных данных.

Очевидно, что при небольшом числе опытов задача более или менее точного определения параметров распределения не может быть решена, так как в этих случаях экспериментальный материал содержит в себе значительный элемент случайности, а, следовательно, и все параметры, вычисленные на его основе, так же будут случайными. При наличии небольшого числа экспериментальных данных может быть поставлена только задача об определении так называемых «оценок» или «подходящих значений» для искомых параметров, т.е. таких приближенных значений, которые при массовом применении приводили бы в среднем к меньшим ошибкам, чем другие.

Существуют различные методы решения задачи оценивания параметров распределения, но на практике наиболее широко применяются два основных метода – метод наименьших квадратов и метод максимального правдоподобия.

Вопрос 1. Обработка результатов наблюдений по методу наименьших квадратов

Метод наименьших квадратов, разработанный знаменитыми математиками К. Гауссом и А. Лежандром, берет свое начало от задач геодезии и астрономии.

Пусть на основании эксперимента требуется установить зависимость некоторой физической величины от физической величины . Например, зависимость пути, пройденного телом, от времени; начальной скорости снаряда от температуры снаряда и т.п. Допустим, что имеются результаты независимых опытов, представленные в виде статистической таблицы:

			...
			...

Изобразим экспериментальные точки на координатной плоскости (рисунок 1).

П усть из теоретических или физических соображений, связанных с существом явления или просто с внешним видом наблюдаемой зависимости, выбран общий вид функции , зависящий от нескольких числовых параметров

Требуется так выбрать параметры , чтобы кривая наилучшим образом изображала зависимость, полученную в опыте.

Данная задача может быть решена с использованием метода наименьших квадратов, при котором требование наилучшего согласования кривой и экспериментальных точек сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от «сглаживающей» кривой обращалась в минимум.

Назовем погрешностью или ошибкой –го измерения величину отклонения наблюдаемого значения от теоретического значения , т.е.

,

где .

Тогда согласно методу наименьших квадратов функция выбирается таким образом, чтобы сумма квадратов погрешностей была минимальной, т.е.

.

Определим параметры , от которых зависит функция , исходя из метода наименьших квадратов. Для этого запишем функцию как функцию не только аргумента , но и параметров :

.

Требуется выбрать так, чтобы выполнялось условие:

. (1)

Из формулы (1) следует, что сумма квадратов погрешностей зависит от параметров , т.е.

, (2)

причем .

В равенстве (2): и – заданные числа (экспериментальные данные), а параметры – неизвестные числа, подлежащие определению, исходя из условия минимума , т.е. сумму квадратов погрешностей можно рассматривать как функцию переменных и исследовать ее на экстремум.

Таким образом, задача свелась к нахождению значений , при которых функция имеет минимум.

Продифференцируем функцию , задаваемую равенством (2), по переменным и приравняем полученные производные к нулю:

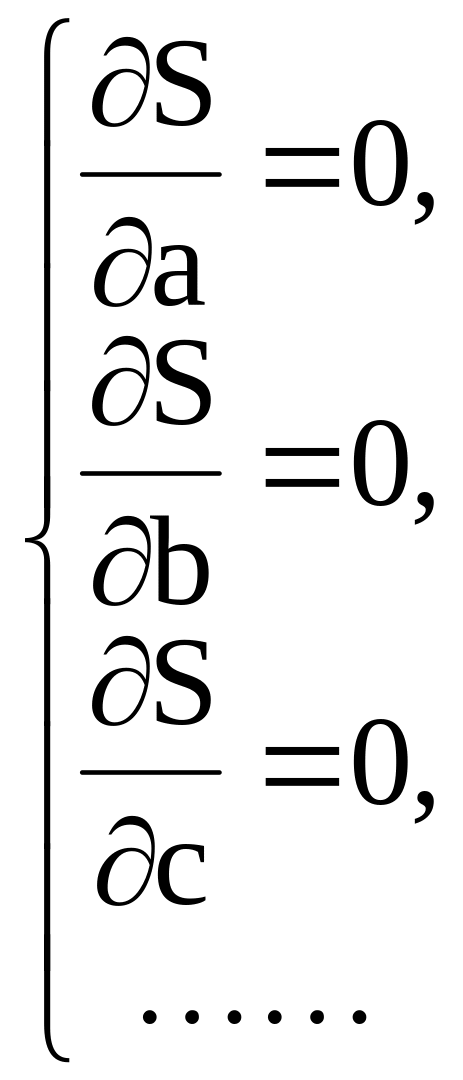(3)

Система уравнений (3) содержит столько же уравнений, сколько неизвестных , но решить систему (3) в общем виде нельзя, т.е. необходимо задать конкретный вид функции .

Рассмотрим часто встречающийся на практике случай, когда функция линейна.