14. Проверка на нормальность закона распределения вероятности результата измерения с помощью гистограмм.

Функция влияния – это зависимость изменения метрологических характеристик средств измерения от изменения влияющего фактора или от изменения совокупности влияющих факторов.

Гистогра́мма (в фотографии) — это график распределения полутонов изображения, в котором по горизонтальной оси представлена яркость, а по вертикали — относительное число пикселов с данным значением яркости.

Изучив гистограмму, можно получить общее представление о правильности экспозиции, контрасте и цветовом насыщении снимка, оценить требуемую коррекцию как при съёмке (изменение экспозиции, цветового баланса, освещения либо композиции снимка), так и при последующей обработке.

Критерий согласия Писона (Х² – хи-квадрат). Гипотеза о соответствии или несоответствии эмпирического закона распределения вероятности. Алгоритм проверки на нормальность закона распределения.

Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.

Статистика критерия

Для проверки критерия вводится статистика:

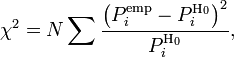
где  — предполагаемая вероятность попадания в -й интервал,  — соответствующее эмпирическое значение,  — число элементов выборки из -го интервала,  — полный объём выборки. Также используется расчет критерия по частоте, тогда:

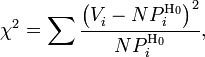
где  — частота попадания значений в интервал. Эта величина, в свою очередь, является случайной (в силу случайности ) и должна подчиняться распределению .

16. Ошибки перго рода. Ошибка второго рода.Вероятность этих ошибок при проверке на нормальность закона распределения. Графики плотности распределения вероятности (хи-квадрат).

Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.

Пусть дана выборка   из неизвестного совместного распределения  , и поставлена бинарная задача проверки статистических гипотез:

где   — нулевая гипотеза, а   — альтернативная гипотеза. Предположим, что задан статистический критерий

,

сопоставляющий каждой реализации выборки   одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:

1. Распределение   выборки 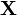  соответствует гипотезе  , и она точно определена статистическим критерием, то есть  .

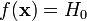2. Распределение   выборки   соответствует гипотезе  , но она неверно отвергнута статистическим критерием, то есть  .

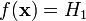3. Распределение   выборки   соответствует гипотезе  , и она точно определена статистическим критерием, то есть  .

4. Распределение   выборки   соответствует гипотезе  , но она неверно отвергнута статистическим критерием, то есть  .

Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. ^[

Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы   и  , то ошибки первого родапревратятся в ошибки второго рода и наоборот. Тем не менее, в большинстве практических ситуаций путаницы не происходит, поскольку принято считать, что нулевая гипотеза   соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей) — например, что обследуемый человек здоров, или что проходящий через рамку металлодетектора пассажир не имеет запрещённых металлических предметов. Соответственно, альтернативная гипотеза   обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная, требующая какой-либо реакции.

С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.

Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.

В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.

Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.

Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).

Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.

Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.

В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.

Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.