8. Обнаружение и исключение ошибок (нормальный закон, функция Лапласа, правило «трех сигм»).

Надежность эргономической системы, в которую входят человек, окружающая среда, объект измерений и средство измерений, не безгранична. В ней могут происходить сбои, отказы аппаратуры, скачки напряжения в сети питания, сейсмические сотрясения, отвлечение внимания оператора, описки в записях и многое другое, не имеющее отношения к измерениям. В результате появляются ошибки , вероятность которых, как следует из теории надежности больших систем, не так уж мала. При однократном измерении ошибка может быть обнаружена только путем логического анализа или сопоставления результата с априорным представлением о нем. Установив и устранив причину ошибки, измерение можно повторить. При многократном изменении одной и той же величины постоянного размера ошибки проявляются в том, что результаты отдельных измерений заметно отличаются от остальных. Иногда это отличие настолько большое, что ошибка очевидна. Остается понять и устранить ее причину или просто отбросить этот результат как заведомо неверный. Если отличие незначительное, то это может быть следствием, как ошибки, так и рассеяния отсчета, а, следовательно, показания и результата измерения, которые, согласно основному постулату метрологии, являются случайными. Нужно поэтому иметь какое-то правило, руководствуясь которым принимать решения в сомнительных случаях. После того, как все влияющие факторы учтены, и все поправки в показания внесены, рассеяние результатов при многократном измерении одной и той же физической величины постоянного размера нередко бывает следствием множества причин, вклад каждой из которых незначителен по сравнению с суммарным действием всех остальных. Центральная предельная теорема теории вероятностей утверждает, что результат измерения при этом подчиняется так называемому нормальному закону: 

кривые плотности распределения вероятности которого при различных значениях дисперсии показаны на рис. 15. 

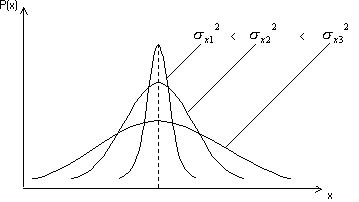
Рис.15. Графики плотности распределения вероятности отсчета при различных дисперсиях.

В теории вероятностей квадратичное отклонение σx случайной величины x (от ее математического ожидания) определяется как квадратный корень из дисперсии Dx и называют также стандартным отклонением величины x. Для любой случайной величины x с математическим ожиданием mx и квадратичным отклонением σx вероятность отклонения x от mx, больших по абсолютной величине k·σx, k > 0, не превосходит 1/k2 (неравенство Чебышева). В случае нормального распределения указанная вероятность при k = 3 равна 0.0027. В практических задачах, приводящих к нормальному распределению, чаще всего пренебрегают возможностью отклонения от среднего, большего 3·σx.

Однократное измерение (роль априорной информации и пять ее вариантов).

Необходимым условием проведения однократного измерения служит наличие априорной информации. К ней относится, например, информация о виде закона распределения вероятности показания и мере ее рассеяния, которая извлекается из опыта предшествующих измерений. Без априорной информации выполнение однократного измерения бессмысленно. Предварительно проводится тщательный анализ априорной информации. В ходе этого анализа уясняется физическая сущность изучаемого явления, уточняется его модель, определяются влияющие факторы. ^

Априо́ри (лат. a priori — буквально «от предшествующего») — знание, полученное до опыта и независимо от него (знание априори, априорное знание), т.е. знание, как бы заранее известное

Необходимым условием проведения однократного измерения является наличие априорной информации. К априорной относятся:

1. информация о виде закона распределения вероятно­сти показания и мере его рассеяния, которая извлекается из опыта предшествующих измерений;

2. информация о том, насколько значение измеряемой величины может отличаться от результата однократного измерения, которая может быть представлена классом точ­ности прибора;

3. информация о значении аддитивной и мультиплика­тивной поправки 9_i. Если значение поправки не известно,то оно учитывается ситуационной моделью, согласно кото­рой значение поправки может быть любым с одинаковой вероятностью в пределах от 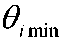до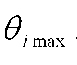 .