26. Оцінювання коефіцієнта кореляції

Коефіцієнт кореляції r не є нормально розподіленою випаковою величиною, його областю визначення є інтервал [-1;1]. Найчастіше відмінність розподілу коефіцієнта кореляції від нормального виражена при тісному зв’язку між змінними, тобто коли коф кореляції за абсолютним значенням близький до 1.

Щоб мати змогу оцінити коефіцієнт кореляції у разі коли його значення не наближене до 0, Фішер у 1921 році запропонував такий метод

Для оцінки коефіцієнта кореляції спочатку перейдемо від випадкової змінної r до випадкової змінної z:

Фішер довів, що випадкова змінна z розподілена за нормальним законом є математичним сподіванням:

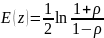
Де -істинне значення коефіцієнта кореляції для генеральної сукупності та дисперсією:

Стандартна вибіркова похибка випадкової величини z буде рівна:

а відповідно гранична вибіркова похибка z при заданому значенні довірчої ймовірності ρ –

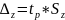
Припустімо, 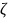– невідоме значення випадкової величини z, яке відповідає істинному значенню коефіцієнта кореляції . Тоді довірчий інтервал для змінної має вигляд:

Де 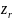-значення випадкової величини z, яке відповідає вибірковому значенню коефіцієнта кореляції r.

Для зручності ми ввели позначення:

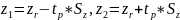
випадкової величини z, яке відповідає вибірковому значенню кофа кореляції r

Тоді 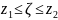, здійснимо обернене перетворення від змінної z до змінної r за формулою:

Отримаємо довірчий інтервал для істинного значення коефіцієнта кореляції генеральної сукупності:

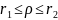
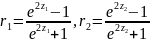
Якщо значення r наближене до 0, тобто зв'язок між змінними слабкий, то його розподіл наближається до нормального. У такому разі похибку коефіцієнта кореляції визначають за формулою

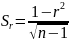
27. Перевірка значущості параметрів зв’язку між змінними

Гіпотеза – це судження про генеральну сукупність. Здебільшого такі судження стосуються невідомого закону розподілу або параметрів відомого розподілу.

Сформульовану гіпотезу називають нульовою, протилежну гіпотезу називають конкуруючою.

Статистичне доведення здійснюється за такою схемою:

1. на підставі даних формулюємо нульову гіпотезу, яку модна обґрунтувати або спростувати

2. Вибираємо критерій – спеціально підібрану випадкову величину K, точний або наближений розподіл якої відомий і яка слугує для перевіряння нульової гіпотези. Розподіли: нормальний, Стьюдента, Фішера-Снедекора, .

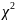3. Вибираємо рівень значущості – імовірність відхилення згідно з вибраним критерієм істинної гіпотези

4. Знаходимо Критичні значення статистики 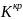, які відповідають рівеню значущості .

5. На підставі даних вибірки обчислюємо емпіричне значення статистики

6. Робимо висновок про доречність застосування нульової гіпотези: якщо емпіричне значення статистики попадає в критичну область, то нульову гіпотезу відкидають, позаяк вона суперечить даним вибірки; в іншому випадку немає підстав відкидати нульову гіпотезу.

Правостороння критична область:

Лівостороння критична область: .

Якщо розподіл статистики симетричний відносно 0 і є підстави вибрати симетричну відносно нуля критичну область, використовують рівняння:

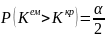
Доцільність застосування нульової гіпотези:

• Гіпотеза істинна, і в результаті проведеного стат доведення ми її приймаємо.

• Гіпотеза хибна, і в результаті проведеного стат доведення ми її відкидаємо.

• Гіпотеза істинна, і в результаті проведеного стат доведення ми її відкидаємо.

• Гіпотеза хибна, і в результаті проведеного стат доведення ми її приймаємо

1. Перевіряння статистичної значущості кофа кореляції.

Для коефіцієнта кореляції формулюється нульова гіпотеза, що реальний коефіцієнт кореляції в генеральній сукупності рівний нулю (ρ =0).

Критичне значення 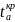цієї статистики при заданому рівні значущості а=0,01 знаходимо за таблицями нормального розподілу. , то нульову гіпотезу відхиляють, і з довірчою імовірністю 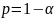, вважають, коф кореляції генеральної сукупності відмінний від 0; якщо ж , то з імовірність з немає підстав відкидати нульову гіпотезу. У другому разі, щоб перевірити нульову гіпотезу, використовують статистику:

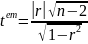
Критичне значення цієї статистики при заданому рівні значущості знаходимо за таблицями розподілу Стьюдента з n-2 ступенями вільності. Висновок аналогічно до попереднього.

2) Для коефіцієнта регресії формулюється така нульова гіпотеза: коефіцієнт регресії генеральної сукупності .

Щоб перевірити гіпотезу про статистичну значущість коефіцієнта регресії b₁ використаємо

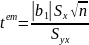
Ця статистика має розподіл Стьюдента з n-2 ступенями вільності. У разі, коли перевіряння нульових гіпотез стосовно стат значущості кофа кореляції та регресії з великою довірчою імовірністю дає змогу зробити висновок про їх статистичну незначущість, будувати та досліджувати ПЛКРМ для вивчення зв’язку між змінними недоцільно.