Метод неопределённых мно-лей Лагнранжа.
Использ для определен реакци связи мех. сист. Вычислив вариац связи, получ
Умножим вариацию
на мно-ль
получим:
P-кол-во
связей.
Построим функцию Лагранжа:
Т.к
,
выб его таким, чтобы удовлетвор ур-ю и
равен-ва 0. Тогда
.
16. Ур-е Лагранжа 1-го рода. Рассм. мех.сис-му, состоящ. из N материальн.точек. На эту мех.сис-му наложено р-связей идеальных. Число степеней свободы r = 3N-p.
=1,2…p.
Вычислим
вариацию функц
ур-:
Умножим
кажд.ур-е на множитель
и сложим эти ур-я,
тогда
получ.:
Bз
нашего утверждения следует, что
Если на М.т действуют
активные и пассивные силы, то ур-е движ
выглядит след образ:
Это и есть ур-е Лагранжа 1-го рода.- дифф ур-ния движ механ. сис, к-рые запис в проекциях на декарт оси и содержат. множ Лагранжа.
17. Общее ур-е механики.
Расс сист из n
М.т запиш з-н Ньютон :
Допуст связи
-
идеальны, тогда раб на вирт перемещ =0
умнож обе части
скалярн на
– это и есть общ
ур-е мех. Оно показ, что в люб мом врем
сум элемент работ ативн сил и сил инерц
=0, если связи не идеальны, то общ ур мех
выгл след образ:
18. Реш зад о движ по накл пл-ти в поле сил тяж на основ ур-и Лагранжа 1-го рода.
h,
Ур-я связи:
.
=>
=>
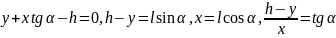Реш сист и получ:
Решим ур-е :
19. Реш задач о движ двух тел связ нер нитью перек через блок на основ общ ур-я механ.
Это
машина Атвуда. Длина нити=
,
трением в блоке пренебр, нить нерастяж.
Ур-е связи x1+x2+
– общ ур динам.
Из ур-я связи:
Получаем:
20. Анализ прим о движ тел, брош под углом в поле сил тяж, мет вариац функци дейцствия.
Ф-я действ имеет
вид
,
где L-ф-я
Лагранжа
=>
огр перв порядком
малости по
:
=
=
тогда
учтём ГУ (
)
=>
Внесём z0 под производ и вынесем, получим:
= 0 –общ ур-е мех.
Принцип мин действия - вариация ф-ции действия => истинный путь будет минимальным.
21. Вариацион принцип.Ур-е Лагранжа-Эйлера.
Принц
наименьш действия -
истинным среди рассматр возможных движ
сист явл то, для котор физ велич, наз
действием, имеет мин знач.
=
=учтём ГУ(
)
и применим фор Ньютон-Лейбниц к под
интегра выраж:
интегр =0 если под
интегр выр =0
Поскольку пределы выб произв образ:
– ур-е Лагранжа –
Эйлера (ур-е Лагранжа 2-го рода)
22. На основ ур-я Л-Э получ ур-е колеб ММ и М.т под действ упр силы.
Есть ММ у него
обобщён корд
Ф-я связи
Далее М.т – есть пруж маятник
Обобщ коорд-
,
=>
23. Ур-е Л-Э для сист с многим степ свободы.
+
= учтём ГУ (
)=
применим фор Ньютон-Лейбниц к под интегра выраж:
интегр =0 если под интегр выр =0
Поскольку пределы выб произв образ:
– ур-е Лагранжа –
Эйлера (ур-е Лагранжа 2-го рода)
24. Обобщ коорд, скор и импульса. Цикл коорд. ЗС обощ имп. Обобщ коорд - совок независ параметр, с помощ которых опис полож тела относ выбр СО в люб момент времени.Число обощ коорд определ числом степ свободы тела. Обобщ сокрости - произв по времени от обощ коорд.
Обобщ имп - произв лагранжеана по обощ сокрости.
Цикл координаты – обобщ коорд мех. сист не вход явно в характерист ф-ии Лагранжа. Налич цикл коорд упрощ процесс интегриров системы т.е для цикл коорд
ЗС обощ имп: дадим
всем радиус вектор одно приращ, котор
не буд влиять на ур-е движ:
С - const
Ф-я Лагранжа измен,
если скор пост
т.к приращ не влияет на ур-е движ, то
вариац ф-и Лагр =0 =>
=>
первые слаг =0 тогда
– обобщ импулс
сист пост велич.
25.Опис движ М.т в потенц сфер-симетр поле в поля корд в форм Лагр.
Обощ
коорд-
ф-я связи
,
=>
1-е слаг сила инерц,
2-е радиаль сила.
26. Ф-я Гамельтона. Привести примеры на её определ.
Выч полная произв от ф-и Лагр по врем:
Перейд
к обобщ имп c
пом ур-я Л-Э:
,
если нет зав от врем то
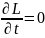
Ф-я
Гамельтона:
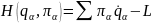
– физ смысл –полн
энергия системы.
Примеры
вычисл: 1)
2)
,
выраз
27. Реш задач Кеплера в формализме Лагранжа.
Задача кеплера свод к реш задач движ М.т в центр поле, запиш функ Лагр для М.т в цент поле:
,
,
=>
1-е слаг сила инерц, 2-е радиаль сила.
Запиш
пол энерг как сум кин и пот, замен
на M
И
Находим
t
затем
28. Законы Кеплера.
1) траектория планет явл элипс, солнце нах в -1м из их фокусов
2) секториальная скорость постоянна, радиус вектор планет за равные промеж врем опис равные площади:
-const
док-во:
3)
T
- периоды, а - большие полуоси.
29.
Осн элем опис линей многомер колеб в
форм Лагр.
Многомер сист – сист с S-степ свободы, для получ данных колеб сист исполь многомер вектор и матрицы.
Матр
-
симметр и вход в кин и потенц энерг
соотв.
S=2 =>
тогда:
Реш:
после подств получ: (
-
)
Ур-е имеет реш,
если храктерст ур-е:
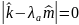
Это ур-е на собств частоты колеб системы.
30. Ур-е колеб линей многомер сист в форм Лагр в лин приближ.
Лин
приближ - это раз в ряд Макларена син и
кос:
т.к ф-я Лагр определ с точ до конст, то
их не учит при подст. Тогда ф-я Лаг выгл:
коэф
-
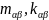коэф матриц соотв.
в силу учёта
порядков малости получим:
=> ур-е колеб:
Ур-е колеб многомер сист в лин приближ.
31. Опред собств частот многомер колеб сист в форм Лагр в лин приближ.
ур-е колеб: его реш
где
Сост хар-е ур-е: – решим его относ лямбда. Получили сист лин однородн уравнен
Кажд собств частоте соотв частн решение:
32. Реш у р-й многомер колеб сист в ф в лин приближ.
Перейдя
к действ. части получ:
-
нах 1- B
,
,
Находим
=
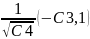
Находим
запис получ действи часть как обще реш,
строим граф и анализ. Колеб могут
происход в фазе либо противофазе.
33. Нормальные колебания.
Нормальные колебания – это малые колеб отдельн мод.
,
Если переписать ф-ю Лагранжа в норм коорд:
,
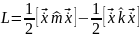Получим ур-е колеб отдельных мод (норм колеб)
34. Постр ф-ю Лагранж дял 2-го ММ в лин приближ.
,
Обощ коорд
Тогда
Распиш син и кос, конст, выше 2-го пор малости отбросим все компоненты.
35. Опред собств частоты двойного ММ.
Допустим длины нитей и массы одинак.
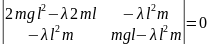
36. Реш ур-е колеб двойного ММ.
Перейдя к действ. части получ:
- нах 1-е B
,
,
Находим =
37. Вариац принц в формал Гамельтона. Ур-е движ мех сист в канон форме.
=>
ГУ( )
Учтём
ГУ и вычс интегралы отдельно, т.к пределы
интегрир выбр произв образом, то интеграл
=0, если его под интеграл выр-е = 0, т.к
обобщё имп и обощ коорд независ др от
друга, то
когда кажд слаг при вариации =0
Получаем
и
38. Опис движ М.т в потенц сфер-симметр поле в форм Гамельтона.
Обобщ коорд- ф-я связи ,
–из форм Лагр выр
имп
, подстав
39. Скобки Пуассона.Опредл скобок для комп имп.
Скоб Пуа - это оператор-коммутатор.
L=[rp] r=rx+ry+rz
подставить вверх опред, раскр опред
и покомпонентно представлять кажд про-е
Примиер:
40. Св-ва скобок Пуассона.
2)
3)
4)
5)
6)
7)
Доп св-ва
1)
2)
41. З-н сохран физ велич в формализме Гамельтона.
Взяли про-ю ф-ии
по врем и прирав к ней же прибавил скобку
пуасоона. Получ:
Если явной зависимости нет от врем, то ЗСЭ выполняется.