Критическое напряжение. Пределы применимости формулы Эйлера.
Пределы применимости формулы Эйлера
Казалось
бы, что полученные в предыдущих параграфах
результаты решают задачу проверки
сжатого стержня на устойчивость; остается
выбрать лишь коэффициент запаса
.
Однако это далеко не так. Ближайшее же
изучение числовых величин, получаемых
по формуле Эйлера, показывает, что она
дает правильные результаты лишь в
известных пределах.
На
рис.1 приведена зависимость величины
критических напряжений, вычисленных
при различных значениях гибкости для
стали 3, обычно применяемой в металлических
конструкциях. Эта зависимость
представляется гиперболической кривой,
так называемой «гиперболой Эйлеpa»:
При
пользовании этой кривой надо вспомнить,
что представляемая ею формула
получена
при помощи интегрирования дифференциального
уравнения изогнутой оси, т. е. в
предположении, что
напряжения в стержне в момент потери
устойчивости не превосходят предела
пропорциональности.
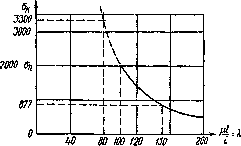Рис.1.
Гиперболическая зависимость критического
напряжения от гибкости стержня
Следовательно, мы не имеем права пользоваться величинами критических напряжений, вычисленных по формуле Эйлера, если они получаются выше этого предела для данного материала. Иначе говоря, формула Эйлера применима лишь при соблюдении условия:
или
Если из этого
неравенства выразить гибкость
,
то условие применимости формул Эйлера
получит иной вид:
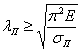
Подставляя
соответствующие значения модуля
упругости и предела пропорциональности
для данного материала, находим наименьшее
значение гибкости, при которой еще можно
пользоваться формулой Эйлера. Для стали
3 предел пропорциональности может быть
принят равным
,
поэтому, для стержней из этого материала
можно пользоваться формулой Эйлера
лишь при гибкости
т. е. большей, чем 100 %
Для
стали 5 при
формула
Эйлера применима при гибкости
;
для чугуна — при
,
для сосны — при
и
т. д. Если мы на Рис.1 проведем горизонтальную
линию с ординатой, равной
,
то она рассечет гиперболу Эйлера на две
части; пользоваться можно лишь нижней
частью графика, относящейся к сравнительно
тонким и длинным стержням, потеря
устойчивости которых происходит при
напряжениях, лежащих не выше предела
пропорциональности.
Теоретическое решение, полученное Эйлером, оказалось применимым на практике лишь для очень ограниченной категории стержней, а именно, тонких и длинных, с большой гибкостью. Между тем, в конструкциях очень часто встречаются стержни с малой гибкостью. Попытки использовать формулу Эйлера для вычисления критических напряжений и проверки устойчивости при малых гибкостях вели иногда к весьма серьезным катастрофам, да и опыты над сжатием стержней показывают, что при критических напряжениях, больших предела пропорциональности, действительные критические силы значительно ниже определенных по формуле Эйлера.
Таким образом, надо найти способ вычисления критических напряжений и для тех случаев, когда они превышают предел пропорциональности материалов, например, для стержней из мягкой стали при гибкостях от 0 до 100.