14.Энергия заряженного конденсатора. Энергия и плотность энергии электростатического поля.

Как всякий заряженный проводник, конденсатор обладает энергией, которая равна

W = C ()2/2=Q/2=Q2/(2C), (1) где Q — заряд конденсатора, С — его ем­кость,  — разность потенциалов между обкладками.

Используя выражение (1), можно найти механическую силу, с которой пластины конден­сатора притягивают друг друга. Для этого предположим, что расстояние х меж­ду пластинами меняется, например, на величину Ах. Тогда действующая сила со­вершает работу dA=Fdx , вследствие уменьшения потенциальной энергии системы

F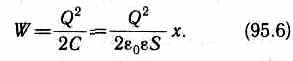 dx=-dW, откуда F=dW/dx. (2)

П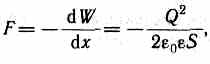 роизводя дифференцирование при кон­кретном значении энергии найдем искомую силу:

где знак минус указывает, что сила F является силой притяжения.

Энергия электростатического поля.

П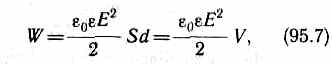 реобразуем формулу (1), выражаю­щую энергию плоского конденсатора по­средством зарядов и потенциалов, вос­пользовавшись выражением для емкости плоского конденсатора (C = 0/d) и раз­ности потенциалов между его обкладками ( =Ed). Тогда получим

где V=Sd — объем конденсатора. Данная ф-ла показывает, что энергия кон­денсатора выражается через величину, ха­рактеризующую электростатическое по­ле,— напряженность Е.

Объемная плотность энергии электро­статического поля (энергия единицы объема)

w=W/V=0E2/2 = ED/2. (95.8)

Выражение (95.8) справедливо только для изотропного диэлектрика, для которого

выполняется соотношение Р=0Е.

Формулы (1) и (95.7) соответствен­но связывают энергию конденсатора с за­рядом на его обкладках и с напряженно­стью поля.

15.

• Электромагни́тное по́ле — фундаментальное физическое поле, взаимодействующее с электрически заряженными телами, а также с телами, имеющими собственные дипольные и мультипольные электрические и магнитные моменты. Представляет собой совокупность электрического имагнитного полей, которые могут, при определённых условиях, порождать друг друга, а по сути являются одной сущностью, формализуемой черезтензор электромагнитного поля.

• Вектор магнитной индукции.

Вектор магнитной индукции является количественной характеристикой магнитного поля.

Магнитная индукция однородного магнитного поля определяется максимальным вращающим моментом действующим на рамку с магн. моментом равным единице, когда нормаль перпендикулярна направлению поля.

П ринцип суперпозиции магнитных полей: если магнитное поле создано несколькими проводниками с токами, то вектор магнитной индукции в какой-либо точке этого поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности:

• Сила Лоренца.

Сила действующая на эл. заряд Q движущийся в магн. поле со скоростью v называется силой Лоренца. F=Q[vB]. Направление силы Лоренца определяется по правилу левой руки. Магнитное поле не действует на покоящийся заряд. Если на движущийся заряд помимо магн. поля действует эл. поле то результирующая сила равна векторной сумме сил. F=QE+Q[vB].

Модуль силы Лоренца равен произведению модуля индукции магнитного поля B(вектор), в котором находится заряженная частица, модуля заряда q этой частицы, ее скорости υ и синуса угла между направлениями скорости и вектора индукции магнитного поля Так как сила Лоренца перпендикулярна вектору скорости частицы, то она не может изменить значение скорости, а изменяет только ее направление и, следовательно, не совершает работы.