5.Связь между напряж.И потенциалом. Потенциалы полей точечного заряда и произв. Заряж. Тела. Потенц. Однородного поля.

Найдем взаимосвязь между напряженно­стью электростатического поля, являю­щейся его силовой характеристикой, и по­тенциалом — энергетической характери­стикой поля.

Работа по перемещению единичного точечного положительного заряда из одной точки в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к равна А=Exdxq0. Та же работа равна A=(1-2)q0=-d Прирав­няв оба выражения, можем записать

Ex=-д/дx. Анлогично Ey=-д/дy, Ez=-д/z. Следовательно Е= Exi+ Eyj+ Ezk, где i, j, k — единичные векторы коорди­натных осей х, у, z. Тогда 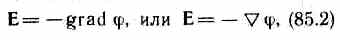т. е. напряженность Е поля равна гради­енту потенциала со знаком минус. Знак минус определяется тем, что вектор на­пряженности Е поля направлен в сторону убывания потенциала.

Д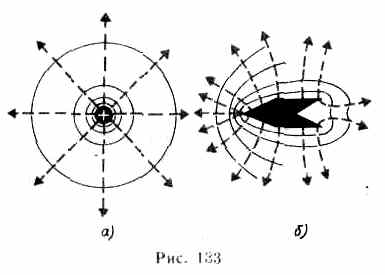 ля графического изображения рас­пределения потенциала электростатиче­ского поля, как и в случае ноля тяготения, пользуются эквипотенциальны­ми поверхностями — поверхностями, во всех точках которых потенциал  имеет одно и то же значение.

Если поле создается точечным заря­дом, то его потенциал, согласно, =(1/40)Q/r. Таким образом, эквипотенциальные поверхности в данном случае — концентрические сферы.

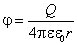С дру­гой стороны, линии напряженности в слу­чае точечного заряда — радиальные пря­мые. Следовательно, линии напряженно­сти в случае точечного заряда перпенди­кулярны эквипотенциальным поверхно­стям.

Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью  :

Потенциал однородного поля: φ = W_п / q = -E_xx + C Значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала. Этот уровень выбирают произвольно.

6. Работа сил элктростат. Поля по переносу точечного заряда. Циркуляция и ротор электростат. Поля

Э лементарная работа, совершаемая силой F при перемещении точечного электрического заряда qпр из одной точки электростатического поля в другую на отрезке пути dl , по определению равна

г де   - угол между вектором силы F и направлением движения dl. Если работа совершается внешними силами, то dA=0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда qпр из точки “а” в точку “b” будет равна…

г де   - кулоновская сила, действующая на пробный заряд qпр в каждой точке поля с напряженностью Е. Тогда работа…

Пусть заряд   перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии   в точку “b”, удаленную от q на расстоянии   (рис 1.12).

К ак видно из рисунка   тогда получим

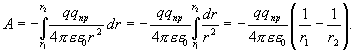
Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно

Работа электростатических сил по любому замкнутому контуру равна нулю. т.е. циркуляция электростатического поля по любому контуру равна нулю. Возьмем любую поверхность S, опирающуюся на контур Г.

По теореме Стокса: 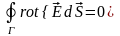так как это для любой поверхности

S, то

Существует тождество: . т.е. силовые линии электростатического поля не циркулируют в пространстве.

7. т-ма гауса для поля вектора E(r). Диверг. Электростат. Поля. Ур-е Пуасона для потенц. Электростат. Поля

Теорема Гаусса — основная теорема электродинамики, которая применяется для вычисления электрических полей. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью.

Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду. , где Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.

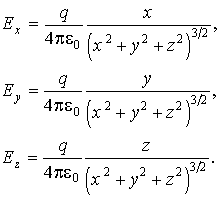  Теорема Гаусса для вектора напряженности электростатического поля   может быть сформулирована и в дифференциальной форме.      Действительно, рассмотрим поле точечного электрического заряда  , расположенного в начале координат:      Из соотношения  следует

          Легко проверить, что для  , то есть для точки наблюдения, в которой нет электрического заряда, справедливо соотношение: (1.55)      Математическая операция в левой части соотношения (1.55) имеет специальное название "дивергенция векторного поля  и специальное обозначение

Уравнение Пуассона — эллиптическое ду в частных производных, которое, среди прочего, описывает электростатическое поле. Это уравнение имеет вид:

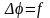
где Δ — оператор Лапласа или лапласиан, а f — действительная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

В декартовой системе координат оператор Лапласа записывается в форме и уравнение Пуассона принимает вид: Если f стремится к нулю, то уравнение Пуассона превращается в ур-е Лапласа: где Ф — электростатический потенциал, — объёмная плотность заряда, а — диэлектрическая проницаемость вакуума.

В области пространства, где нет непарной плотности заряда, имеем: =0 и уравнение для потенциала превращается в уравнение Лапласа:

8.

Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов).

Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный заряд, помещённый в этом поле. Пробный заряд должен быть малым, чтобы не повлиять на характеристику электростатического поля.

В силу принципа суперпозиции потенциал всей совокупности зарядов равен сумме потенциалов, создаваемых в данной точке поля каждым из зарядов в отдельности: : *

Величина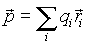 называется электрическим дипольным моментом системы зарядов.

Э лектрич. дипольным моментом или просто дипольным моментом системы зарядов q _i называется сумма произведений величин зарядов на их радиус-векторы.

Обычно дипольный момент обозначается латинской буквой d или латинской буквой p.

Дипольный момент имеет чрезвычайное значение в физике при изучении нейтральных систем. Действие электрического поля на нейтральную систему зарядов и электрическое поле создано нейтральной системой определяются в первую очередь дипольным моментом. Это, в частности, касается атомов и молекул.

Нейтральные системы зарядов с отличным от нуля дипольным моментом называют диполями.

Свойства: Всего определенный выше дипольный момент зависит от системы отсчета. Однако для нейтральной системы сумма всех зарядов равна нулю, поэтому зависимость от системы отсчета исчезает.

С амый диполь состоит из двух одинаковых по абсолютной величине, но противоположных по направлению зарядов + q и-q, которые находятся на определенном расстоянии r друг от друга. Дипольный момент тогда равна по абсолютной величине qr и направлен от положительного до отрицательного заряда. В случае непрерывного распределения заряда с плотностью   дипольный момент определяется интегрированием