3 .Рассмотрим некоторые физические свойства жидкостей и параметры, используемые при расчете процессов химической технологии, протекаю­щих в покоящейся или движущейся жидкости.

1. Плотность и удельный вес. Масса единицы объема жидкости назы­вается плотностью и обозначается через ρ:

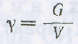ρ=[кг/м³]

Вес единицы объема жидкости называется удельным весом и обозначается через γ, т. е.

γ=[н/м³]

т.к. G=m*g, то γ=ρ*g

pV= NRT=(m/M)RT – Ур-е Клайперона.

При N=const, PV/T=P₀V₀/T₀ ;

Норм. условия: P₀=1атм=760мм.рт.ст.=101,325КПа

T₀=273,15К

V₀=22,4*N=22,4*m/M, м³ ;

ρ₀=M/22,4; → ρ_t,p= ρ₀*(T₀*P)/(T*P₀);

pV=zNRT, где z=f(π,τ); π=p/p_кр, τ=T/T_кр; π-приведен. давление, τ-приведен. температура.

Для нефтяных жидкостей:

ρ²⁰₄=ρ²⁰_{нефт.продукта}/ρ⁴_H20 ; ρ_t2=ρ_t1-a*(t₂-t₁); a-температ. коэф-т;

а=0,001828-0,00132* ρ²⁰₄ ;

2. Давление;

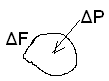ΔP-сила гидростат. давления, кот. действует перпендикулярно площади ΔF;

ΔF- элементарная площадка;

ΔP/ΔF – среднее гидростатическое давление; P=lim (ΔP/ΔF) –давление дан.точки жидкости (напряжение гидростатического давления) при ΔF→0.

Давление в любой точке ж-ти одинаково по всем направлениям. В противном случае мы будем наблюдать перемещение ж-ти внутри объема ж-ти.

p= ρgH= γH; p=[н/м²=Па];

1. атм. – физ. атмосфера (760мм.рт.ст.=101,3КПа);

2. ат. – технич. атмосфера (735,6мм.рт.ст.=98,1КПа);

Различают абс. давление(P_абс), атмосф-ое(P_атм), изб-ое(P_изб), вакуумное(P_вак):

P_абс= P_изб +P_атм ;

P_абс= P_атм +P_вак ;

3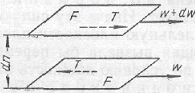 . Вязкость - свойство жидкости оказывать сопротивление усилиям, вызывающим относительное перемещение ее частиц.

Представим себе слой жидкости, находящийся между двумя параллель­ными горизонтальными пластинами (Рис. 1). Для того чтобы пере­мещать верхнюю пластину относительно нижней в горизонтальной пло­скости с постоянной скоростью, нужно прилагать некоторую постоянную касательную силу, так как вязкая жидкость оказывает сопротивление такому перемещению.

Рассмотрим два параллельных слоя площадью F каждый, причем расположенный выше слой движется со скоростью (W+dW), большей, чем скорость расположенного ниже слоя, на бесконечно малую величину dW.

Опыт показывает, что касательная сила T, которую надо прилагать к верхнему слою для его равномерного сдвига относительно нижнего (или противоположно направленная сила трения T, с которой нижний слой сопротивляется перемещению верхнего), тем больше, чем больше градиент скорости dW/dn, характеризующий изменение скорости, при­ходящееся на единицу расстояния по нормали между слоями. Кроме того, каждая из сил T пропорциональна площади соприкосновения F слоев. Следовательно:

T= μF*dW/dn; τ=T/F=-μ*dW/dn; τ- напряжение внутреннего трения(напряжение сдвига или касат. напряжение);

μ- динамический коэф-т вязкости или просто вязкость. μ=[Па*с]; μ=[пз]-пуаз или μ=[спз]-сантипуаз; 1Па*с=10пз=1000спз.

ν=μ/ρ= (μ*g)/γ; ν-кинематический коэф-т вязкости или кинемат.вязкость; ν=[м²/с]; ν=[ст]-стокс ; 1 м²/с=10⁴ ст.

Вязкость капельных жидкостей значительно снижается с возрастанием температуры. Вязкость газов, наоборот, увеличивается с ее повышением.

Причины различного влияния температуры на вязкость капельных жидкостей и газов, а также отмеченного характера влияния давления на вязкость последних обусловлены тем, что вязкость газов имеет молекулярно-кинетическую природу, а вязкость капельных жидкостей в основном зависит от сил сцепления между молекулами. Вязкость газов про относит. высоких давлениях увеличивается с увеличением давления.

Различают ньютоновские (норм-ые) ж-ти – они подчиняются законам внутреннего трения и неньютоновские – они обладают аномальными свойствами и не подчиняются з-нам Ньютона.

Вязкость влияет на режим течения ж-ти (критерий Рейнольдса), на гидравлич. сопротивление, на выбор методов интенсификации химико-технологич. процессов.

4. Поверхностное натяжение – оно представляет собой работу, требуемую для образования единицы новой поверхноти:

σ=[дж/м²]=[н*м/м²]=[н/м];

4. Дифференциальные уравнения равновесия Эйлера

В объеме жидкости, находящейся в покое, выделим элементарный параллелепипед объемом dV с ребрами dx,dy и dz расположенными парал­лельно осям координат x,y и z. Сила тяжести, действующая на параллелепипед, выражается произведением его массы dm на ускорение

свободного падения g, т. е. равна gdm. Сила гидростатического давления на лю­бую из граней параллелепипеда равна произведению гидростатического давления p на площадь этой грани. Будем считать, что давление p является функцией всех трех координат: p=f(x,y,z). Выясне­ние вида этой функции, т. е. закона распределения гидростатического давле­ния по объему жидкости, и является на­шей задачей.

Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю.

Рассмотрим сумму проекций сил на ось z. Сила тяжести направлена вниз, параллельно оси z. Поэтому при выбранном положительном направ­лении оси z сила тяжести будет проектироваться на эту ось со знаком минус: -gdm=-gρdV=-ρgdxdydz;

Сила гидростатического давления действует на нижнюю грань парал­лелепипеда по нормали к ней, и ее проекция на ось z равна pdxdy. Если изменение гидростатического давления в данной точке в направлении оси z равно ∂p/∂z, то по всей длине ребра dz оно составит (∂p/∂z)dz. Тогда гидростати­ческое давление на противоположную (верхнюю) грань равно (p+(∂p/∂z)dz) и проекция силы гидростатического давления на ось z: -(p+(∂p/∂z)dz)dxdy.

Проекция равнодействующей силы давления на ось z: pdxdy-(p+(∂p/∂z)dz)dxdy=-(∂p/∂z)dzdxdy

Сумма проекций сил на ось z равна нулю, т.е. –ρgdxdydz-(∂p/∂z)dxdydz=0;

или, учитывая, что объем параллелепипеда dxdydz=dV≠0 (величина, заведомо не равная нулю), получим: -ρg-(∂p/∂z)=0

Проекции сил тяжести на оси x и y равны нулю. Поэтому сумма проек­ций сил на ось x: pdydz-(p+(∂p/∂x)dx)dydz=0

откуда после раскрытия скобок и сокращения находим: -(∂p/∂x)dxdydz=0

ИЛИ -(∂p/∂x)=0

Соответственно для оси y: -(∂p/∂y)dxdydz=0

или -(∂p/∂y)=0

Таким образом, условия равновесия элементарного параллелепипеда выражаются системой уравнений:

-(∂p/∂x)=0

-(∂p/∂y)=0

-ρg-(∂p/∂z)=0

Полученные уравнения представляют собой дифференциальные уравнения равновесия Эйлера.

Для получения закона распределения давления во всем объеме покоя­щейся жидкости следует проинтегрировать систему уравнений. Интегралом этих уравнений является основное уравнение гидростатики.