2.1.2. Свойства энтропии

1) Как следует из (2.4), Н = 0 только в двух случаях: (а) какая-либо из p(A_j) = 1; однако, при этом из (А.7) следует, что все остальные р(А_i) = 0 (i≠j), т.е. реализуется ситуация, когда один из исходов является достоверным (и общий итог опыта перестает быть случайным); (b) все р(А_i) = 0, т.е. никакие из рассматриваемых исходов опыта невозможны, поскольку нетрудно показать, что (р ∙ log р) = 0 во всех остальных случаях, очевидно, что Н > 0.

2) Очевидным следствием (2.1) будет утверждение, что для двух независимых опытов α и β

Энтропия сложного опыта, состоящего из нескольких независимых, равна сумме энтропии отдельных опытов.

В справедливости (2.5) можно убедиться непосредственно: Пусть опыт α имеет п исходов А₁, А₂, … А_п, которые реализуются с вероятностями р(А₁), р(А₂), ... р(А_п), а событие β - т исходов B₁, В₂, ... В_т с вероятностями р(В₁), р(В₂), ... р(В_т). Сложный опыт α ^ β имеет п∙т исходов типа A_iB_j (i = 1... n, j = 1... т). Следовательно:

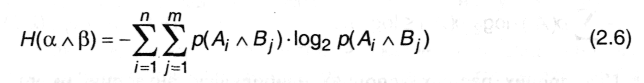
Поскольку α и β - независимы, то независимыми окажутся события в любой паре A_i ^ B_j. Тогда, согласно (А.9),

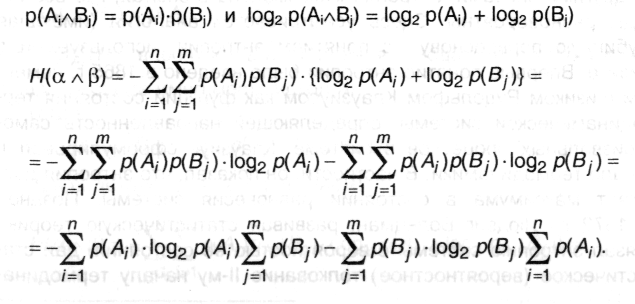
В слагаемых произведено изменение порядка суммирования в соответствии со значениями индексов. Далее, по условию нормировки (А.7):

а из (2.4)

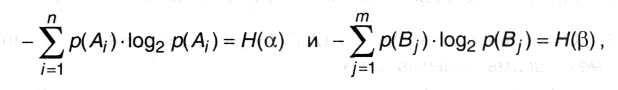
окончательно имеем:

что и требовалось доказать.

Теперь рассмотрим ситуацию, когда имеются два опыта с одинаковым числом исходов п, но в одном случае они равновероятны, а в другом - нет. Каково соотношение энтропии опытов? Примем без доказательства* следующее утверждение:

* При необходимости доказательство можно найти, например, в книгах: А.М. и И.М. Яглом [49, с.73-75]; Л. Бриллюэн [7, с.34-36].

При прочих равных условиях наибольшую энтропию имеет опыт с равновероятными исходами.

Другими словами, энтропия максимальна в опытах, где все исходы равновероятны. Здесь усматривается аналогия (имеющая глубинную первооснову!) с понятием энтропии, используемой в физике. Впервые понятие энтропии было введено в 1865 г. немецким физиком Рудольфом Клаузиусом как функции состояния термодинамической системы, определяющей направленность самопроизвольных процессов в системе. Клаузиус сформулировал II начало термодинамики. В частности, он показал, что энтропия достигает максимума в состоянии равновесия системы. Позднее (в 1872 г.) Людвиг Больцман, развивая статистическую теорию, связал энтропию системы с вероятностью ее состояния, дал статистическое (вероятностное) толкование II-му началу термодинамики и, в частности, показал, что вероятность максимальна у полностью разупорядоченной (равновесной) системы, причем, энтропия и термодинамическая вероятность оказались связанными логарифмической зависимостью. Другими словами, в физике энтропия оказывается мерой беспорядка в системе. При этом беспорядок понимается как отсутствие знания о характеристиках объекта (например, координат и скорости молекулы); с ростом энтропии уменьшается порядок в системе, т.е. наши знания о ней. Сходство понятий и соотношений между ними в теории информации и статистической термодинамике, как оказалось позднее, совершенно не случайно*.

* Подробнее об этом можно причитать в книгах Л.Бриллюэна [7] и Р.Л.Стратоновича [39].

Кстати, результат, полученный в рассмотренном выше примере 2.1, иллюстрирует справедливость формулы (2.7).