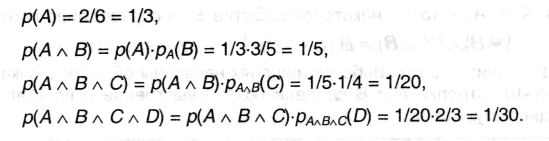A.3. Условная вероятность

Попробуем построить обобщенную формулу для вероятности суммарного события (А.5) на ситуацию, когда отдельные события А и В могут оказаться совместными, т.е. произойти одновременно. В этом случае p(A v B) ≠ p(A) + p(B). Действительно: пусть по-прежнему событие А выполняется при т₁ из п равновероятных исходов опыта, а событие В - при m₂ из тех же п возможных исходов. Однако из-за того, что возможно совместное наступление А и В, исходы m₁ и т₂ окажутся не полностью различными, т.е. среди них могут быть одни и те же. Тогда суммарное количество благоприятных исходов т ≤ т₁ + т₂ и, следовательно, p(A v B) ≤ р(А) + р(В).

Пусть среди т₁ и т₂ имеются т' общих исходов; очевидно, это те случаи, когда А и В наступают одновременно. Следовательно, вероятность совместного события

а общее количество различных благоприятных исходов оказывается равным т = т₁ + т₂ - т'. Тогда вероятность

Окончательно:

Таким образом, при определении вероятности суммы двух событий (A v B) в общем случае требуется находить и вероятность их произведения (А ^ В). Это несложно сделать, если события А и В независимы - в этом случае можно воспользоваться формулой (А.9), подстановка которой в (А. 12) дает:

Легко видеть, что (А.5) оказывается частным случаем (А. 12) при условии несовместности А и B - тогда р(А ^ В) = 0.

Пример А.5

Какова вероятность вынуть козыря или туза из колоды 36 карт, если козырной объявлена одна из мастей?

Событие А - получение козыря - имеет вероятность р(А) = 9/36 = 1/4, поскольку карт одной масти 9. Событие B - получение туза - имеет вероятность р(В) = 4/36 = 1/9, поскольку тузов 4; однако из них один - козырный (т.е. реализуются и А и B); вероятность его появления р(А ^ В) = р(A) ∙ р(B) = 1/36. Тогда, согласно (А.13), р(А ^ В) = р(А) + р(В) - р(A) ∙ р(В) = 1/4 + 1/9 - 1/36 = 12/36 = 1/3

Теперь при нахождении вероятности произведения событий р(A ^ B) попробуем учесть то обстоятельство, что события А и В не обязательно могут быть независимыми - очевидно, это наиболее общий случай. Отсутствие независимости случайных событий означает, что одно из них оказывает влияние на другое, т.е. вероятность второго события зависит от того, произошло ли первое. Например, вы случайно встретили знакомого на вечеринке (событие В); однако решение пойти на эту вечеринку (событие А) вы приняли случайно, выбирая из нескольких возможностей; таким образом, случайное событие В оказывается следствием случайного события А.

Вероятность события В при условии, что влияющее на него событие А имело место, называется условной вероятностью.

Обозначать условную вероятность будем р_А(В). Объективности ради следует заметить, что вероятность любого случайного события зависит от каких-то условий, при которых возможно его наступление или ненаступление. Например, условием того, что вероятность выпадения всех цифр игральной кости одинакова и равна 1/6, является ее правильная геометрическая форма и однородность материала. Если условия изменятся (например, форма будет не куб, а параллелепипед), то изменится и вероятность. Просто условились считать вероятность событий, для которых условия не изменяются в различных сериях опытов, безусловной; если же условия могут изменяться - используется термин «условная вероятность». Достаточно очевидным представляется также утверждение: если А и B независимы, то р_A(В) = р(В). Более того, данное утверждение можно считать математически точным определением понятия «независимые события»;

Два случайных события А и В являются независимыми, если их условные вероятности равны безусловным, т.е. р_А(В) = р(В) и р_В(А) = р(А).

Пусть из п равновероятных исходов событие А реализуется т способами, из которых k являются благоприятными и для наступления события В, связанного с А. Тогда, очевидно:

Вероятность совместного выполнения событий А ^ В равна

Но

Окончательно имеем:

Полученное выражения является наиболее общим правилом умножения вероятностей; выражение (А.9), очевидно, оказывается частным случаем (А.14) при условии, что А и B независимы. Подстановка полученного выражения в формулу (А.12) позволяет получить общее правило сложения вероятностей:

Перечислим (без доказательства) некоторые свойства условной вероятности:

1) условная вероятность р_A(iB) может быть как больше безусловной р(В), так и меньше ее (т.е. событие А может как понижать вероятность В, так и повышать ее); однако, всегда 0 ≤ Р_A(B) ≤ 1. Для ситуации, когда А с необходимостью влечет за собой В (например, А - выпадение четверки при бросании игральной кости, а B - выпадение четной цифры) будем использовать обозначение «» (А  B - читается «A влечет B»). Очевидно, если А  B, то р_A(B) = 1. Если А и B несовместны, р_А(В) = 0;

2) если B  B', то р_А(В) ≤ р_A(B');

3) для дополнительных событий р_A(В) = 1 – p_A(B);

4) если B и С несовместны, то p_A(B v С) = р_А(В) + р_А(С).

Пример А.6*

* Примеры А.6 и А.7 взяты из книги А.М Яглома. и И.М. Яглома [49.С.44-45]

Имеется три урны, содержащие белые и черные шары, причем, в первой урне 2 белых и 4 черных шара, во второй - 3 белых и 3 черных, в третьей - 4 белых и 2 черных. Из одной из урн (неизвестно из какой) наугад вынут шар. Какова вероятность того, что шар оказался белым при условии, что он вынут из первой урны?

Пусть событие А - вытаскивание белого шара, а B - то, что он вынут из первой урны. Из всех имеющихся шаров событию А благоприятствует 9; из которых лишь 2 благоприятствуют событию B. Таким образом р_А(В) = 2/9.

Пример А.7

На карточках отдельными буквами написано слово «ПАПАХА». Карточки переворачивают, перемешивают и случайным образом открывают подряд 4 из них. Какова вероятность получить таким путем слово «ПАПА»?

Пусть событие А - извлечение первой «П», событие В - извлечение второй «А», С - третьей «П» и D-четвертой «А». Тогда интересующее событие можно записать как A^В^С^D; его вероятность можно найти, применяя несколько раз формулу (А.14):