А.2. Сложение и умножение вероятностей

Сложение вероятностей независимых, несовместных событий

Пусть среди возможных равновероятных исходов благоприятными оказывается любое из событий А или B, причем А и В - независимы (т.е. между ними отсутствуют причинно-следственные связи - А не влияет на B и наоборот) и несовместны (т.е. они не могут наступить одновременно, а наступает лишь одно из них). Путь из общего числа равновероятных исходов п событие А осуществляется т₁ числом способов, а событие В - т₂. Тогда

Спрашивается, как найти вероятность события С = (А или В)*? С называют также суммой событий A и В. Очевидно, общее число способов, которым может реализоваться С равно m₁ + т₂. Следовательно,

* Используя формализм математической логики, можно записать С = A v B.

Вероятность какого-либо одного из двух исходов независимых и несовместных событий равна сумме их вероятностей

Например, какова вероятность вынуть красный или зеленый шар в рассмотренном выше примере? р(А)= 5/10, р(В) = 3/10, следовательно, р(А v B) = 8/10.

Формулу (А.5) легко обобщить на произвольное число благоприятных исходов. Пусть из п несовместных событий k являются благоприятными исходами, причем, вероятности каждого составляют р₁, р₂,..., p_k. Тогда вероятность наступления любого (хотя бы одного) из благоприятных событий будет равна

Из соотношения (А.6) условия нормировки вероятностей (А.2) легко вывести два следствия:

Следствие 1. Если общее количество всех возможных исходов равно п с вероятностями p₁,..., р_n, то

поскольку появление хоть какого-то из исходов достоверно. Это выражение можно считать обобщением условия нормировки.

Следствие 2. Если возможных исходов всего два (А или B), то наступление одного означает не наступление второго. Поэтому любой из них является противоположным другому (записывается В = ; читается «не А»). Поскольку р(А) + р(В) = 1, то р(B) = 1 - р(А) или

Например, если определили ранее (пример А.2), что вероятность вытащить красный или зеленый шар составляет 8/10, то это означает, что вероятность не вытащить любой из них будет равняться 1 - 8/10 = 2/10.

Умножение вероятностей независимых совместных событий Пусть событие А реализуется т₁ способами из п₁ равновероятных исходов одного опыта, а событие В - т₂ способами из п₂ равновероятных исходов другого опыта, независимого от первого. Спрашивается, какова вероятность одновременного наступления обоих событий (или сложного события С, состоящего в наступлении и А и B)? То есть хотим определить вероятность совместного события С = (А и B)*. Часто С называют произведением событий А и B. Поскольку каждому из п₁ исходов первого опыта соответствует п₂ исходов второго, то общее количество возможных равновероятных исходов, очевидно, становится равным п₁∙п₂. Из них благоприятными окажутся т₁∙т₂ исходов. Следовательно, вероятность совместного события оказывается равной:

* Используя формализм математической логики можно записать С = А ^ B.

Вероятность одновременного наступления двух благоприятных исходов независимых событий равна произведению их вероятностей

Пример А.3

Какова вероятность выбросить 2 раза подряд по 6 очков в двух бросках кубика (или, что эквивалентно, при однократном броске двух кубиков)? Поскольку р(А) = р(В) = 1/6, то р = 1/6 ∙ 1/6 = 1/36.

Как и в случае сложения вероятностей, формула (А.9) может быть обобщена на произвольное число совместных благоприятных событий в k независимых опытах. Если вероятности их наступления в каждом из опытов р₁, p₂,..., p_k, то вероятность совместного события будет равна:

Следствие 3. Поскольку р_j ≤ 1, очевидно, что р ≤ p_j, т.е. вероятность совместного события не может превышать вероятность любого из них.

Следствие 4. Нахождение среднего для значений случайных независимых величин. Рассмотрим частную ситуацию, когда случайным событием является числовое значение некоторой величины. Например, число, указанное на грани кубика; сумма выигрыша в лотерею; номер этажа, на котором живет человек, масса атома химического элемента и т.п. Пусть этих значений п и они образуют дискретный ряд x₁, х₂, ..., x_n. Среди этих значений могут оказаться одинаковые. Пусть таких групп одинаковых значений k. Очевидно, k ≤ п. Попробуем найти ответ на вопрос: каково среднее значение величины х? Например, сколько в среднем очков выпадает при одном броске кубика? Будем исходить из определения среднего значения:

Однако эта же сумма может быть получена, если провести суммирование по группам одинаковых значений:

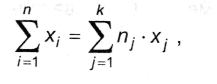
где n_j - количество значений в группе j. Тогда

поскольку отношение п_j/п есть ни что иное, как относительная частота появления результата из группы j, которая в пределе (при п→) превращается в вероятность р_j. Таким образом, окончательно получаем, что

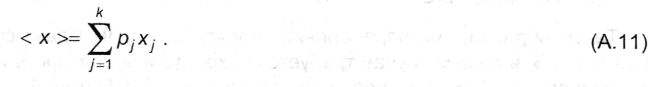
Пример А.4

Найти среднее количество очков, выпадающее при однократном броске игральной кости. Поскольку все р_j = 1/6, а значения x_j = 1, 2.....6, согласно (А.1).

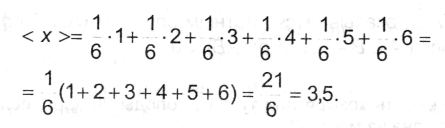
Величина, определяемая соотношением (А.11), называется взвешенным средним для выборки х_1; х₂, ..., x_k.