Контрольные вопросы и задания

1. Приведите примеры терминов, имеющих несколько трактовок в различных науках, технике, быту.

2. Приведите примеры процессов, используемых для передачи информации, и связанных с ними сигналов кроме указанных в тексте.

3. Приведите примеры неоднозначного и однозначного соответствия между сообщением и содержащейся в нем информацией.

4. Почему хранение информации нельзя считать информационным процессом?

5. В чем состоит различие понятий «приемник сообщения» и «приемник информации»?

6. Органы чувств человека ориентированы на восприятие аналоговой информации. Означает ли это, что человек не может воспринимать информацию дискретную?

7. Приведите примеры знаков-символов. Могут ли символы образовывать алфавит?

8. В шестнадцатиричной системе счисления используются цифры А, В, С, D, Е и F. Следует ли эти знаки считать символами?

9. В тексте данной главы разграничиваются понятия «знак», «буква», «символ». Как соотносится с ними понятие «цифра»?

10. В чем состоит смысл и значение теоремы отсчетов?

11. Какое количество отсчетов за 1 с необходимо производить цифровому звукозаписывающему устройству, если требуется обеспечить качество записи (а) телефона; (b) лазерного диска.

12. Как следует понимать термины «оцифровка изображения» и «оцифровка звука»? Какими устройствами производятся данные операции?

13. Приведите примеры преобразований типа D₁ → D₂, при которых информация, содержащаяся в исходном сообщении, может не сохраняться.

14. Почему для представления дискретных сообщений в качестве базового выбирается двоичный алфавит?

15. Почему компьютер является универсальным устройством по обработке информации?

16. В чем состоит и как проявляется несимметричность непрерывной и дискретной форм представления информации?

Глава 2. Понятие информации в теории Шеннона

Материал данной главы опирается на понятия и соотношения теории вероятностей. Для тех, кто не знаком с этой теорией, необходимые ее элементы изложены в приложении А. Текст главы содержит ссылки на некоторые формулы из этого приложения - они в качестве первого индекса имеют букву «А».

2.1. Понятие энтропии

2.1.1. Энтропия как мера неопределенности

Случайные события могут быть описаны с использованием понятия «вероятность» (см. приложение А). Соотношения теории вероятностей позволяют найти (вычислить) вероятности как одиночных случайных событий, так и сложных опытов, объединяющих несколько независимых или связанных между собой событий. Однако описать случайные события можно не только в терминах вероятностей.

То, что событие случайно, означает отсутствие полной уверенности в его наступлении, что, в свою очередь, создает неопределенность в исходах опытов, связанных с данным событием. Безусловно, степень неопределенности различна для разных ситуаций. Например, если опыт состоит в определении возраста случайно выбранного студента 1-го курса дневного отделения вуза, то с большой долей уверенности можно утверждать, что он окажется менее 30 лет; хотя по положению на дневном отделении могут обучаться лица в возрасте до 35 лет, чаще всего очно учатся выпускники школ ближайших нескольких выпусков. Гораздо меньшую определенность имеет аналогичный опыт, если проверяется, будет ли возраст произвольно выбранного студента меньше 18 лет. Для практики важно иметь возможность произвести численную оценку неопределенности разных опытов. Попробуем ввести такую количественную меру неопределенности.

Начнем с простой ситуации, когда опыт имеет п равновероятных исходов. Очевидно, что неопределенность каждого из них зависит от n, т.е. мера неопределенности является функцией числа исходов f(n).

Можно указать некоторые свойства этой функции:

1. f(1) = 0, поскольку при п = 1 исход опыта не является случайным и, следовательно, неопределенность отсутствует;

2. f(n) возрастает с ростом п, поскольку чем больше число возможных исходов, тем более затруднительным становится предсказание результата опыта.

Для определения явного вида функции f(n) рассмотрим два независимых опыта α и β* с количествами равновероятных исходов, соответственно п_α и п_β. Пусть имеет место сложный опыт, который состоит в одновременном выполнении опытов α и β; число возможных его исходов равно п_α ∙ п_β, причем, все они равновероятны. Очевидно, неопределенность исхода такого сложного опыта α ^ β будет больше неопределенности опыта α, поскольку к ней добавляется неопределенность β; мера неопределенности сложного опыта равна f(n_α ∙ n_β). С другой стороны, меры неопределенности отдельных α и β составляют, соответственно, f(n_α) и f(n_β). В первом случае (сложный опыт) проявляется общая (суммарная) неопределенность совместных событий, во втором - неопределенность каждого из событий в отдельности. Однако из независимости α и β следует, что в сложном опыте они никак не могут повлиять друг на друга и, в частности, α не может оказать воздействия на неопределенность β, и наоборот. Следовательно, мера суммарной неопределенности должна быть равна сумме мер неопределенности каждого из опытов, т.е. мера неопределенности аддитивна:

* Для обозначения опытов со случайными исходами будем использовать греческие буквы (α, β и т.д.), а для обозначения отдельных исходов опытов (событий) - латинские заглавные (А, В и т.д.).

Теперь задумаемся о том, каким может быть явный вид функции f(n), чтобы он удовлетворял свойствам (1) и (2) и соотношению (2.1)? Легко увидеть, что такому набору свойств удовлетворяет функция log(n), причем можно доказать, что она единственная из всех существующих классов функций. Таким образом:

за меру неопределенности опыта с п равновероятными исходами можно принять число log(n).

Следует заметить, что выбор основания логарифма в данном случае значения не имеет, поскольку в силу известной формулы преобразования логарифма от одного основания к другому.

переход к другому основанию состоит во введении одинакового для обеих частей выражения (2.1) постоянного множителя log_b а, что равносильно изменению масштаба (т.е. размера единицы) измерения неопределенности. Поскольку это так, имеется возможность выбрать удобное (из каких-то дополнительных соображений) основание логарифма. Таким удобным основанием оказывается 2, поскольку в этом случае за единицу измерения принимается неопределенность, содержащаяся в опыте, имеющем лишь два равновероятных исхода, которые можно обозначить, например, ИСТИНА (True) и ЛОЖЬ (False) и использовать для анализа таких событий аппарат математической логики.

Единица измерения неопределенности при двух возможных равновероятных исходах опыта называется бит*.

* Название бит происходит от английского binary digit, что в дословном переводе означает «двоичный разряд» или «двоичная единица».

Таким образом, нами установлен явный вид функции, описывающей меру неопределенности опыта, имеющего п равновероятных исходов:

Эта величина получила название энтропия. В дальнейшем будем обозначать ее Н.

Вновь рассмотрим опыт с п равновероятными исходами. Поскольку каждый исход случаен, он вносит свой вклад в неопределенность всего опыта, но так как все п исходов равнозначны, разумно допустить, что и их неопределенности одинаковы. Из свойства аддитивности неопределенности, а также того, что согласно (2.2) общая неопределенность равна log₂ п, следует, что неопределенность, вносимая одним исходом составляет

где р = - вероятность любого из отдельных исходов.

Таким образом, неопределенность, вносимая каждым из равновероятных исходов, равна:

Теперь попробуем обобщить формулу (2.3) на ситуацию, когда исходы опытов неравновероятны, например, р(А₁) и р(А₂). Тогда:

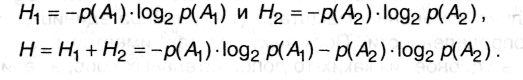
Обобщая это выражение на ситуацию, когда опыт α имеет п неравновероятных исходов А₁, А₂... А_п, получим:

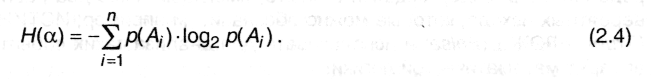
Введенная таким образом величина, как уже было сказано, называется энтропией опыта ос. Используя формулу для среднего значения дискретных случайных величин (А.11), можно записать:

А^(α) - обозначает исходы, возможные в опыте α.

Энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.

Для практики формула (2.4) важна тем, что позволяет сравнить неопределенности различных опытов со случайными исходами.

Пример 2.1

Имеются два ящика, в каждом из которых по 12 шаров. В первом -3 белых, 3 черных и 6 красных; во втором - каждого цвета по 4. Опыты состоят в вытаскивании по одному шару из каждого ящика. Что можно сказать относительно неопределенностей исходов этих опытов?

Согласно (2.4) находим энтропии обоих опытов:

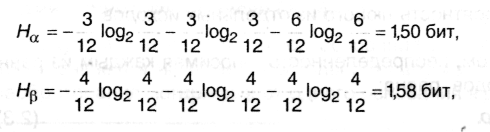
Н_β > Н_α, т.е. неопределенность результата в опыте β выше и, следовательно, предсказать его можно с меньшей долей уверенности, чем результат α.