Модели структурные и функциональные

Состояние прототипа - это совокупность свойств его составных частей, а также его собственных. Состояние - «моментальная» фотография прототипа для выбранного момента времени. С течением времени состояние может изменяться - тогда говорят о существовании процесса. В соответствии со сказанным возможно построение модели состояния и модели процессов. Модели первого типа называются структурными моделями, второго типа - функциональными моделями. Примерами структурных моделей являются чертеж какого-либо устройства, схема компьютера, блок-схема алгоритма и пр. Примерами функциональных моделей являются макет, демонстрирующий работу чего-либо; протез. Важнейшим классом функциональных моделей являются модели имитационные.

Имитационное моделирование - метод исследования, основанный на том, что изучаемый прототип заменяется ее имитатором - натурной или информационной моделью - с которым и проводятся эксперименты с целью получения информации об особенностях прототипа.

Примером натурной имитационной установки может служить аэродинамическая труба, позволяющая исследовать воздушные потоки, обтекающие транспортное средство (самолет, автомобиль, тепловоз и пр.) при движении. В качестве имитаторов могут выступать и математические модели, реализованные на компьютере. В настоящее время именно имитационное моделирование оказывается важнейшим методом исследования и прогнозирования в науке, экономике и др. Примерами является моделирование последствий ядерной войны, прогноз погоды, экономические прогнозы и пр.

Модели натурные и информационные

Модели можно отнести к одной из двух групп: натурные (материальные) и информационные (нематериальные). Классификацию по этому признаку удобно представить в графической форме (рис. 10.1).

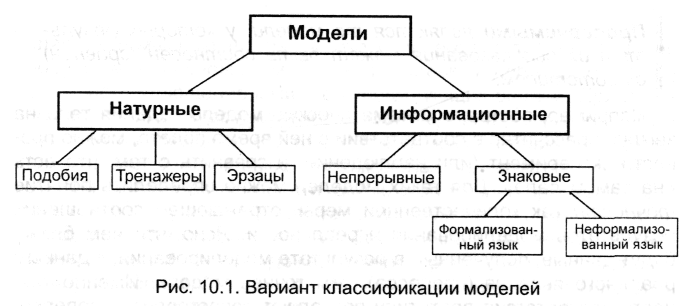
Примерами натурных моделей подобия являются игрушка, манекен, фотография и т.п.

К натурным моделям-тренажерам следует отнести различные устройства, применяемые при подготовке летчиков, водителей и пр., которые имитируют некоторую ситуацию, требующую принятия решений и действий, и позволяют отрабатывать методы ее разрешения.

Модели-эрзацы - это, в первую очередь, протезы, заменяющие и частично выполняющие функции настоящих органов.

Примером непрерывной информационной модели может служить математическая функция и ее график.

Знаковые информационные модели можно было бы назвать также дискретными, подчеркивая то обстоятельство, что информация в них представлена в дискретной форме, т.е. посредством некоторого алфавита и языка. Язык может быть обычным разговорным - с неформализованным синтаксисом. Примерами моделей, построенных посредством такого языка, являются различные описания, характеристики, мнения, толкования и пр.

Формализованные языки, как обсуждалось выше, имеют фиксированный набор лексических единиц (слов) и жесткий синтаксис фраз. Именно этим обеспечивается однозначность понимания смысла фраз и исполнения содержащихся в них указаний. Примером моделей, представленных посредством формализованных языков, может служить математическое описание существующего в природе или человеческом обществе явления, процесса; запись шахматной партии; нотная запись услышанных звуков и пр. Построение знаковой модели является обязательным этапом решения практической задачи с помощью компьютера; в дальнейшем, говоря о моделях в информатике, будем подразумевать именно информационные знаковые модели.