Контрольные вопросы и задания
Почему для описания конечного автомата требуется задание двух автоматных функций? Возможны ли ситуации, когда функция преобразования будет единственной?
Почему рассматриваемые в теории автоматов устройства называются дискретными?
Постройте схемы автоматов, реализующих следующие логические функции:
Предложите вариант соединения комбинационных схем одноразрядного сумматора и полусумматора для построения многоразрядного сумматора.
В чем состоит отличие комбинационных схем и конечных автоматов?
Можно ли считать конечным автоматом: (а) электронный будильник; (b) телевизор с пультом управления; (с) автомат для продажи газированной воды; (d) телефонный аппарат.
Задан конечный автомат с алфавитами X = {а1, а2}, Y = {b1, b2}, Q = {q1, q2}; автоматные функции заданы в виде таблицы:
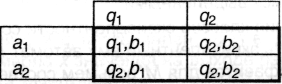
Постройте систему команд автомата, а также представьте его диаграммой. На вход подано слово a1a2a2a3. Определите выходное слово.
Постройте таблицу и диаграмму для элемента задержки, триггера, двоичного счетчика.
Постройте диаграмму для автомата, рассмотренного в примере 9.4.
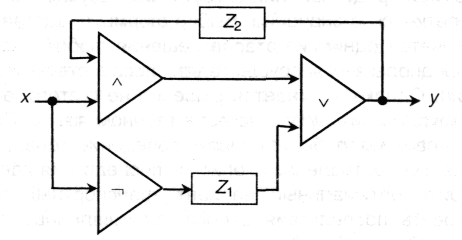
Пользуясь методом устранения задержек, напишите систему канонических уравнений для автомата, схема которого приведена; постройте таблицу преобразований и таблицу автоматных функций, а также постройте диаграмму автомата.
Действие конечного автомата описывается таблицей:
Постройте автоматные функции, а по ним - схему конечного автомата.
Почему описанная в данном разделе система элементов названа полной?
Какие автоматы называются эквивалентными? Какой автомат из эквивалентных является минимальным? Всегда ли возможно построение минимального автомата?
Глава 10. Модели и системы
Рассмотренные в предыдущей главе вопросы, связанные с формализацией представления алгоритмов, безусловно, имеют не только теоретическое значение. Выбор формы представления алгоритма является одним из этапов решения любой задачи, если решение предполагается осуществлять посредством какого-либо исполнителя. Однако начинается решение не с этого, а с постановки (формулировки) задачи на естественном языке. Примерами таких постановок могут быть: описать поведение тела, двигающегося в среде с сопротивлением; описать последствия ядерной войны; построить оптимальный вариант транспортных перевозок; спрогнозировать последствия сброса промышленных отходов в водоем и т.п. Будем считать, что такая постановка осуществлена; и интересны этапы решения задачи, следующие за постановкой, но предшествующие формальному представлению алгоритма. Другими словами, прослеживаем всю последовательность решения задачи с помощью исполнителя и, в частности, компьютера.
Как увидим, интересующие этапы связаны с выделением систем и построением моделей. Эти шаги тесно связаны друг с другом, поскольку выделение системы есть моделирование, а модель, в свою очередь, является системой. Тем не менее, прежде чем обсуждать связи между понятиями «система» и «модель», их взаимопроникновение и взаимообусловленность, рассмотрим их по отдельности.