9.3.3. Эквивалентные автоматы

Автоматы являются устройствами для переработки дискретной информации. При этом характером перерабатываемой информации определяется входной и выходной алфавиты (X и Y); алфавит внутренних состояний (Q) определяется строением автомата и, вообще говоря, он может различаться у разных автоматов с одинаковыми входными и выходными алфавитами. Следовательно, одно и то же преобразование информации может быть осуществлено автоматами с разным числом состояний и, следовательно, посредством различного числа команд. Введем ряд определений:

Состояния q автомата М и q' автомата М' считаются эквивалентными, если оба автомата, получив одну и ту же (любую) входную последовательность символов, перерабатывают ее в одинаковую выходную последовательность.

Автоматы М и М' называются эквивалентными, если для каждого состояния автомата М существует эквивалентное ему состояние автомата М' и наоборот.

Другими словами, эквивалентные автоматы реализуют одинаковые преобразования, но могут иметь различное число внутренних состояний.

Понятие эквивалентности состояний применимо и к одному автомату (формально можно считать, что М и М' совпадают). Для одного автомата эквивалентными будут различные состояния, через которые одна и та же входная последовательность символов преобразуется в одинаковую выходную.

В связи с синтезом схем практический интерес представляет задача построения автомата, выполняющего заданный набор преобразований при минимальном числе внутренних состояний.

Автомат, эквивалентный заданному и имеющий наименьшее из всех возможных число состояний называется минимальным.

Задача построения минимального автомата называется задачей минимизации автомата. Ее решение осуществляется в два этапа: сначала устанавливаются все неэквивалентные состояния исходного автомата, а затем по ним стоится минимальный автомат. В свою очередь, для определения неэквивалентных состояний необходимо выявить классы эквивалентных состояний.

Пусть имеется автомат с множеством внутренних состояний Q, среди которых могут быть эквивалентные. Отношения эквивалентности состояний обладают обычными свойствами эквивалентности, т.е. рефлексивностью, симметрией и транзитивностью. Поэтому множество Q может быть разбито на классы эквивалентности. Процедуру рассмотрим на примере.

Пример 9.5

Пусть имеется конечный автомат, заданный таблицей:

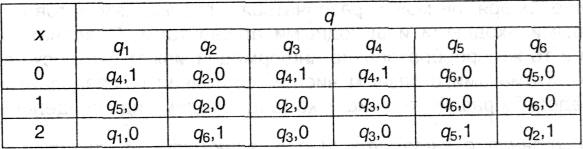
На основе ее составим другую таблицу, клетки которой будут соответствовать всем различным парам q_iq_j (i ≠ j), заполнив ее согласно следующим правилам:

• если два состояния q_i и q_j неэквивалентны (т.е. для какого-либо значения входного символа х значения на выходе различаются), то соответствующая клетка зачеркивается;

• если в состояниях q_i и q_j для каждого х значения на выходе одинаковы, то в клетки записываются все пары состояний q_vq_w (v ≠ w), отличные от q_iq_j, в которые автомат может перейти из q_i и q_j при подаче одного и того же входного символа.

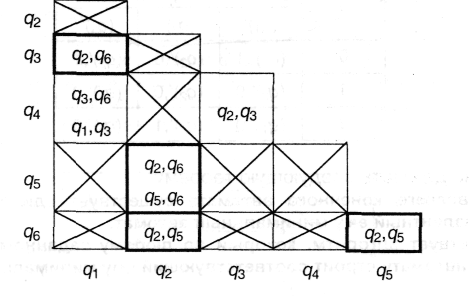
Согласно первому правилу зачеркнутой оказалась, например, клетка, соответствующая паре q₁q₂, поскольку при х = 0 на выходе выдаются разные значения (1 и 0). По второму правилу, например для пары q₅q₆ следует записать пару q₂q₅ из следующих соображений: у q₅ и q₆ все выходные символы одинаковы при одинаковых входных; х = 0 приводит к исходной паре q₅q₆; х = 1 приводит к паре одинаковых состояний q₆q₆.

Подобным образом анализируются остальные сочетания.

Наконец, последующими преобразованиями вычеркиваются клетки, в которых находятся пары, соответствующие уже зачеркнутым ранее клеткам. Например, следует зачеркнуть клетку для пары q₁q₄, поскольку в ней содержится q₃q₆, а также q₃q₄, так как в ней есть q₂q₃. Затем снова нужно зачеркнуть все клетки, которые содержат пары, соответствующие вычеркнутым клеткам. Процедура должна продолжаться до тех пор, пока не сформируется таблица, в которой нельзя вычеркнуть ни одной из оставшихся клеток. Для рассматриваемого примера эти клетки выделены жирной рамкой. Можно доказать, что оставшиеся не вычеркнутыми клетки соответствуют всем парам эквивалентных состояний. Это q₁q₃, q₂q₅, q₂q₆ и q₅q₆. Классы эквивалентности образуются состояниями, которые попарно эквивалентны. В этом случае это {q₁,q₃} и {q₂, q₅, q₆}. Состояния, не вошедшие в эти классы, эквивалентны лишь себе и образуют собственные классы эквивалентности; в рассматриваемом примере это {q₄}. Таким образом, классы эквивалентности оказались выделенными.

После выделения классов эквивалентности состояний для автомата М можно построить эквивалентный ему автомат M'. В качестве входного и выходного алфавитов для М' возьмем соответствующие алфавиты М, а каждому классу эквивалентных состояний М сопоставим одно состояние М'. Для рассмотренного выше примера можно принять (q₁)' ↔ {q₁, q₃}, (q₂)' ↔ {q₂, q₅, q₆}, (q₃)' ↔ {q₄}.

Окончательно получаем таблицу нового автомата М'.

Можно доказать следующую теорему*:

* Интересующихся доказательством можно адресовать к книге Л.А. Шоломова [48, с.125-126].

Для всякого конечного автомата существует единственный эквивалентный ему минимальный автомат. Существует алгоритм, который по любому заданному конечному автомату строит соответствующий ему минимальный.

Можно доказать также, что рассмотренная нами процедура и является тем самым алгоритмом, позволяющим построить минимальный автомат эквивалентный заданному.