9.3.2. Схемы из логических элементов и задержек
При создании конечных автоматов используется несколько типов элементов памяти, из которых основными следует считать элемент задержки, двоичный триггер и двоичный счетчик.
Элемент задержки имеет функцию перехода вида q(ti) = x(ti) и функцию выхода вида y(ti) = q(ti-1). Из них, в частности видно, что y(ti+1) = q(ti) = x(ti), т.е. элемент осуществляет задержку входного сигнала на один такт (поданный на некотором такте сигнал поступит на выход лишь на следующем такте). Задержка используется в линиях обратной связи, когда, например, сигнал подается с выхода схемы на ее вход.
Двоичный триггер имеет два входа х1 и х2. Функция переходов имеет следующий вид: q(ti) = (x1(ti), x2(ti)); ее значения устанавливаются таким образом: (1,0) = 1, т.е. при подаче 1 на вход х, и 0 на вход х2 триггер переходит в состояние 1 и сохраняет это состояние до тех пор, пока оно не будет заменено иным; (0,1) = 0, т.е. 0 на x1 и 1 на х2 переводят триггер в состояние 0; i(0, 0) = i-1, т.е. при обоих нулевых сигналах состояние триггера не изменяется. Одновременная подача единичных сигналов на оба входа триггера исключается конструкцией схемы. Выходная функция триггера при любых состояниях у(ti) = q(ti), т.е. на выход подается текущее состояние триггера, но оно от этого не изменяется. Таким образом, триггер сохраняет сколь угодно долго записанный в него бит информации. Объединения подобных элементов образуют регистры и ячейки памяти, из которых, в свою очередь, строится вся память устройства. Память эта по количеству двоичных элементов, разумеется, конечна.
Двоичный счетчик имеет один вход; он меняет свое состояние на противоположное, если на входе 1, и сохраняет его, если на входе 0. Очевидно, q(ti) = (x(ti), q(ti-1)), причем, (1,1) = 0, (1,0) = 1, (0,1) = 1, (0,0) = 0; y(ti) = q(ti).
Добавлением элементов памяти к базису из логических элементов, использовавшихся при построении комбинационных схем, образует новый базис, который обладает свойством полноты. Под полнотой понимается возможность построения на основе данного базиса схемы, задающей любое отображение последовательностей входных сигналов на последовательности выходных, которое вообще может быть задано дискретным двоичным преобразователем информации с конечной памятью. Другими словами, возможно построение любых схем, поведение которых определяется как входными сигналами, так и их состоянием на предыдущем такте.
Далее будем рассматривать схемы с единственным видом памяти - задержкой (на схемах будет обозначаться Z). Схемы строятся по определенным правилам. Исходными понятиями являются: элемент (логический или задержка) и вход в схему (он называется полюсом). Можно дать следующее индуктивное определение схемы (попутно определяется понятие вершины схемы):
совокупность полюсов, соответствующая некоторому набору входных переменных х1, ... xn, является схемой; вершинами схемы будут ее полюсы;
результат присоединения к вершинам схемы всех входов некоторого базисного элемента есть схема; полюсами будут все полюсы исходной схемы, а вершинами - все вершины исходной схемы и выход присоединенного элемента (рис. 9.4, а);
результат присоединения выхода задержки к некоторому полюсу xk есть схема; ее полюсами будут все полюсы исходной схемы, за исключением xk, a вершинами - все вершины исходной схемы, кроме xk (рис. 9.4, б).
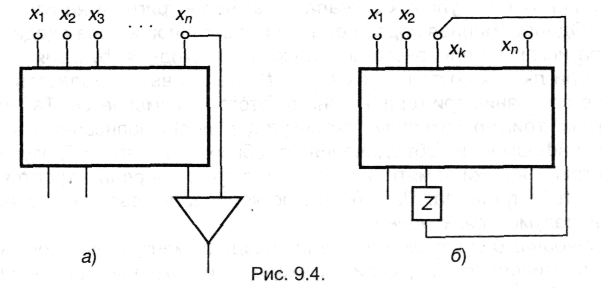
В соответствии с правилами построения схем каждой ее вершине может быть сопоставлена функция, указывающая значение сигнала на некотором такте ti, а каждой задержке Zj - дополнительная функция, указывающая ее состояние на данном такте qj(ti). Значения функций определяются по следующим правилам:
полюсу хr приписывается дискретная функция xr(t), значения которой являются значениями t в такты 0, 1, 2, ...;
вершине, соответствующей выходу логического элемента (рис. 9.4, а), приписывается значение, сформированное этим элементом согласно сигналам на его входе;
если элемент задержки Zj присоединен к вершине, которой приписана некоторая функция f(t), то согласно значениям автоматных функций задержки для состояния задержки принимается qj(ti) = f(ti), а выходу задержки приписывается qj(ti-1);
если задержка присоединяется к полюсу (рис. 9.4, б), то в функциях, приписываемых вершинам и состояниям задержек, функция xk(ti) везде заменяется на qj(ti-1).
Любая правильно построенная схема из логических элементов и задержек обладает следующими двумя свойствами:
каждый вход всякого элемента присоединен либо к полюсу, либо к выходу другого элемента;
в любой циклической цепочке элементов присутствует по крайней мере один элемент задержки.
В отношении схем, содержащих элементы памяти, решаются задачи анализа и синтеза. Задача анализа состоит в том, чтобы по заданной схеме найти реализуемый автомат, т.е. установить все алфавиты, а также явный вид системы канонических уравнений. Задача синтеза является обратной по отношению к задаче анализа: по заданному конечному автомату построить реализующую его схему над выбранным базисом (логические элементы и элементы памяти). В основе анализа схем лежит метод устранения задержек. Его идея состоит в том, что из схемы можно удалить имеющиеся задержки, заменив их дополнительными полюсами, на которые поданы сигналы, соответствующие значениям функции, приписываемые задержке. В результате получается новая схема только из логических элементов с расширенным (по отношению к исходному) входным алфавитом. Для этой схемы строятся автоматные функции и, тем самым, устанавливается вид конечного автомата.
Пример 9.4
Пусть задана схема (рис. 9.5, а), содержащая по одному логическому элементу И, ИЛИ, НЕ и два элемента задержки (на схеме обозначены Z), на вход которой подается сигнал х. Обозначим внутреннее состояние задержек, соответственно, q1 и q2.
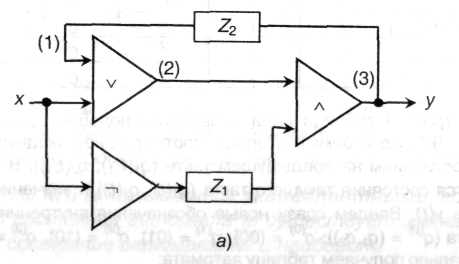
Тогда в соответствии со сформулированными выше правилами для выделенных вершин схемы можно записать:
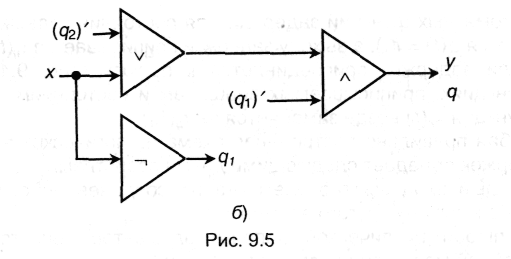
После удаления из исходной схемы задержек перейдем к схеме, представленной на рис. 9.5, б. Она реализует следующие функции:
поэтому канонические уравнения автомата будут иметь вид:
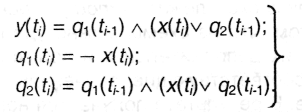
Теперь можно построить представить эти уравнения в виде таблицы значений:
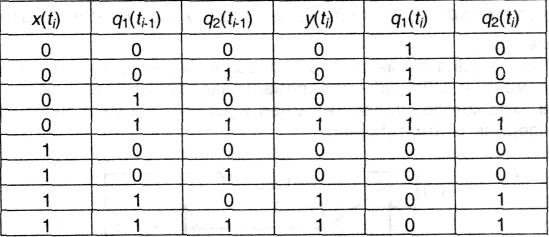
Далее строится таблица команд автомата подобно рассмотренной в примере 9.1. Ее строки и столбцы соответствуют входным символам x(ti) и состояниям на предыдущем такте (q1(ti-1), q2(ti-1)). В клетках размещаются состояния текущего такта (q1(ti), q2(ti)) и значение выходного символа y(ti). Введем сразу новые обозначения внутренних состояний автомата (q(p) = (q1, q2)): q(0) = (00), q(1) = (01), q(2) = (10), q(3) = (11). Тогда окончательно получаем таблицу автомата:
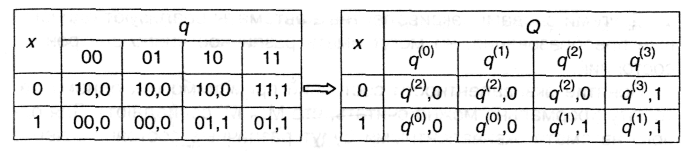
Решение задачи синтеза автомата из логических элементов и элементов задержки производится в обратном порядке: строится система канонических уравнений автомата; автоматные функции представляются в виде таблицы или диаграммы; по ним находится система булевских функций, описывающих работу автомата; по ней - набор логических элементов и связи между ними и, наконец, в них вводятся элементы задержки. Таким образом, теория автоматов позволяет разработать алгоритмические методы перехода от этапа описания характера преобразований, которые должен осуществлять конечный автомат, к конкретным схемным решениям, основанным на использовании рассмотренного выше набора элементов. Это, в свою очередь, дает возможность задачу проектирования новых конечных автоматов формализовать для решения посредством другого конечного автомата, в частности, компьютера. Такая технология действительно существует и широко используется в практике создания новых устройств.