9.3. Конечные автоматы

9.3.1. Способы задания конечного автомата

Комбинационные схемы, хотя и позволяют реализовать любые фиксированные зависимости между входными и выходными сигналами, не могут изменять характера своего поведения (т.е. последовательности обработки данных) - любое такое изменение требует изменения структуры схемы, т.е., по сути, переходу к другой схеме. Решить проблему перестройки работы без изменения структуры схемы возможно, если ввести в нее элементы памяти, которые позволяли бы фиксировать и сохранять промежуточные состояния устройства - в этом случае выходной сигнал будет зависеть не только от входного сигнала, но и от состояния схемы. Если количество таких элементов конечно, то, как указывалось выше, дискретное устройство будет называться конечным автоматом.

Конечным автоматом называется система <X, Y, Q, , >, в которой X и Y являются конечными входным и выходным алфавитами, Q - конечным множеством внутренних состояний, (x, q) - функцией переходов и (x,q) - функцией выходов.

Как указывалось ранее, (x,q) задает порядок преобразования входных символов и состояния автомата на предыдущем такте в состояние на последующем, a (x,q) - преобразования входных символов и состояния автомата на текущем такте в выходной символ. Если q₀ - начальное состояние автомата, а i - номер такта, то его работа описывается системой:

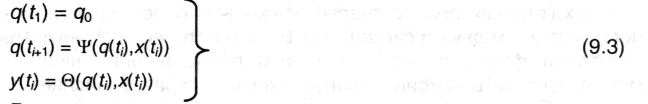
Данные соотношения получили название системы канонических уравнений конечного автомата. Пользуясь ими можно, начиная с q₀, последовательно находить все последующие состояния автомата и выходные символы.

Выделяются два типа автоматов - инициальные и неинициальные. В инициальных автоматах начальное состояние фиксировано (т.е. они всегда начинают работать из одного и того же состояния q₀). В неинициальных автоматах в качестве начального состояния может быть выбрано любое из множества Q; этим выбором определяется дальнейшее поведение автомата.

Представление конкретного конечного автомата фактически сводится к описанию задающих его автоматных функций. Из системы (9.3) следует, что при конечном числе возможных внутренних состояний количество возможных значений автоматных функции также оказывается конечным. Их описание возможно различными способами, наиболее распространенными из которых является табличный и с помощью диаграмм.

В табличном способе автоматные функции задаются двумя конечными таблицами, именуемыми соответственно матрицей переходов и матрицей выходов. В этих таблицах строки обозначаются буквами входного алфавита, а столбцы - буквами внутреннего алфавита (символами, кодирующими внутреннее состояние автомата). В матрице переходов на пересечении строки (x_k) и столбца (q_r) помещаются значения функции  (q_r, x_k), а в матрице выходов - значения функции (q_r, x_k).

Пример 9.2.

По заданному табличному представлению автомата построить систему его команд.

Пусть конечный автомат имеет алфавиты X = {a, b}, Y = {а, b, с}, Q = {1, 2, 3}, а автоматные функции задаются таблицами:

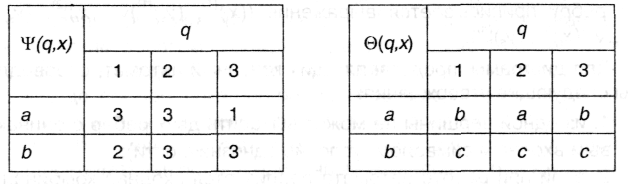
Представленные две таблицы можно объединить в одну, условившись в каждую клетку на первую позицию ставить значение (q_r, x_k), а через запятую на вторую позицию помещать значение (q_r, x_k). В результате получится следующая «сводная» таблица:

Видно, что таблица стала весьма напоминать таблицу, задающую функциональную схему машины Тьюринга (см. п.7.3.3). Из нее легко просматриваются команды преобразования, осуществляемые данным автоматом:

Пусть на начальном такте автомат находится в состоянии q₀ = 1 и на его вход в последующие такты подается последовательность abb. Пользуясь перечнем команд можно установить, что автомат преобразует эту последовательность в bсс и при этом окажется в состоянии 3.

Другой вариант описания автоматных функций - графический. Он обладает большей наглядностью, чем табличный. Состояния автомата <X, Y, Q, , > задается посредством ориентированного графа, который называется диаграммой (точнее, диаграммой Мура). Вершины графа помечены символами из алфавита состояний автомата Q, а каждой команде q_ix_r → q_jy_s соответствует ребро, идущее из вершины q_i в вершину q_j, при этом ребру приписывается метка x_ry_s. Таким образом, ребро возникает в том случае, если автомат, находящийся в состоянии q_i, посредством некоторого входного сигнала x_r может быть переведен в состояние q_j. Если такой перевод возможен при нескольких входных воздействиях (х_г)⁽¹⁾..... (х_r)^(п), и при этом формируются выходные сигналы (y_s)⁽¹⁾,..., (y_s)^(п), то ребру приписывается выражение ((х_r)⁽¹⁾, (y_s)⁽¹⁾) v ((х_r)⁽²⁾, (y_s)⁽²⁾) v...v((x_r)⁽ⁿ⁾,(y_s)⁽ⁿ⁾.

Для диаграмм, представляющих конечный автомат, справедливы следующие утверждения:

1. из одной вершины не может выходить двух ребер с одинаковым входным символом (условие однозначности);

2. если при работе автомата реализуется входная комбинация q_ix_r, то обязательно существует ребро, идущее из вершины q_i помеченное символом х_r (условие полноты);

3. количество вершин и ребер диаграммы является конечным.

Пример 9.3

Построить диаграмму для конечного автомата, описанного в примере 9.1.

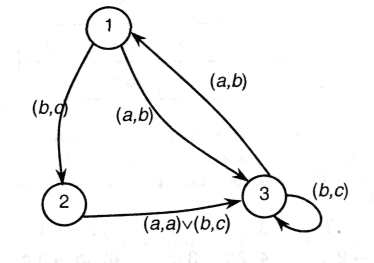
Если на начальном такте автомат находился в состоянии q₀ = 1 и на егo вход в последующие такты подавались символы abb, то, пользуясь диаграммой, можно проследить последовательность преобразований: 1а → 3b → 3с → 3с - выходные символы будут появляться в порядке bсс.