9.2. Дискретные устройства без памяти

Введенное в предыдущем параграфе понятие автомата является достаточно общим. Накладывая ограничения на компоненты X, Y, Q, Ψ, Θ можно получить частные случаи автоматов. Одним из них являются автоматы без памяти, т.е. устройства, в которых не происходит фиксации внутреннего состояния. Очевидно, в этом случае из общего описания должны быть исключены компоненты Q и Ψ; автомат без памяти задается тройкой компонентов < X, Y, Θ>. Соотношение (9.2) принимает вид

т.е. выходной символ на данном такте определяется только входным символом и не зависит от ранее поступивших символов. Следовательно, каждый автомат без памяти реализует единственный преобразователь (оператор), который осуществляет «побуквенный перевод» входных последовательностей символов в выходные.

Пусть имеется дискретное устройство, имеющее п входов х₁.....х_п и т выходов y₁ ..., у_т. Если данное устройство не обладает памятью, то преобразование входных сигналов в выходные описывается системой уравнений:

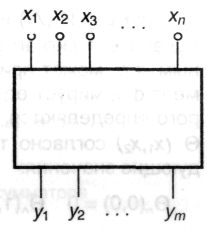
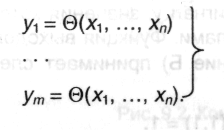
Если входной и выходной алфавиты являются двоичными, то представленная система оказывается системой логических функций, для решения которой можно привлечь аппарат математической логики. Именно такие устройства будем рассматривать в дальнейшем.

Подобные устройства могут быть построены путем соединения некоторого набора элементарных компонентов (элементов). Эти элементы образуют конечный набор, называемый базисом, а входящие в него элементы - базисными. Базис имеет смысл совокупности элементарных (простейших) действий, о которых шла речь в теории алгоритмов, а базисный элемент можно рассматривать в качестве устройства, выполняющее элементарное действие. Если речь идет о двоичных дискретных устройствах, то базисы строятся из элементов, которые реализуют простейшие логические функции. Напомним, что к таким функциям относятся конъюнкция (логическое И - ^), дизъюнкция (логическое ИЛИ - v), импликация (→), сумма по модулю 2 (), эквивалентности (~) и отрицания (логическое НЕ - ,). Однако между простейшими функциями имеются соотношения эквивалентности (см. приложение), позволяющие выразить одни функции через другие. В результате оказывается, что нет необходимости включать в базис все элементы, реализующие простейшие логические функции - достаточно выбрать некоторое минимальное их подмножество. Этому условию удовлетворяет базис, построенных на элементах И, ИЛИ и НЕ - он называется простейшим, а входящие в него элементы - логическими элементами или (логическими вентилями). Схемы элементов приведены на рис. 9.1. Рассмотрим каждый их них по отдельности.

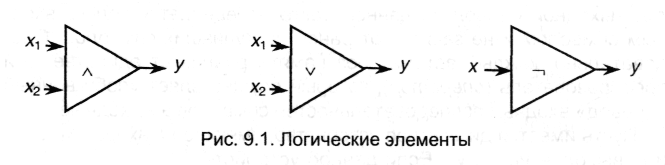
Элемент И (^) имеет два входа, на которые независимо могут подаваться сигналы x₁ и х₂; каждый из сигналов является двоичным, т.е. может принимать одно из двух значений - 1 или 0; элемент формирует единственный выходной сигнал у, значения которого определяются только входными сигналами. Функция выходов  (x₁,x₂) согласно табл. Б.1 (см. приложение Б) принимает следующие значения:

Функция выходов элемента ИЛИ (V) принимает следующие значения:

Логический элемент НЕ () обеспечивает одноместное преобразование (с одним входным сигналом) в соответствии с правилами:

Комбинируя базисные элементы по определенным правилам, можно построить их сложные объединения - схемы (над данным базисом), способные совершать преобразования, соответствующие, вообще говоря, любым логическим функциям. Таким образом, схема есть комбинация базисных элементов, в которой выходы одних элементов присоединяются к входам других. Если в таких объединениях элементов отсутствуют замкнутые контуры (подача сигнала с выхода элемента на один из его же входов), то возникает класс схем, которые называются комбинационными. Говорят, что базис обладает свойством полноты, если схемами над ним может быть реализована любая логическая функция (и, следовательно, любая система логических функций). В частности, таким свойством обладает простейший базис.

Со схемами связано решение двух классов задач - анализа и синтеза. В задачах анализа выявляется логическая функция, реализуемая заданной схемой. Синтез - это, наоборот, построение схемы по заданной конечной логической функции.

Пример 9.1

Определить логическую функцию, реализуемую представленной схемой на рис.9.2.

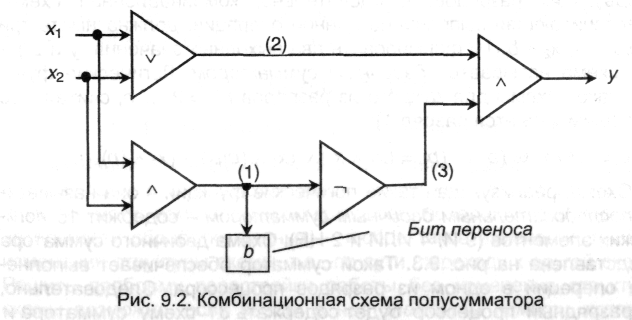
Решение будем вести последовательно, находя значение функции в точках схемы, отмеченных цифрами. Для упрощений используем соотношения из приложения Б.

Таким образом, у = x₁  х₂; b = x₁ ^ х₂). Результаты обработки могут быть представлены в виде таблицы:

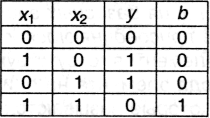
Поскольку перечисленные преобразования являются правилами двоичного суммирования, рассмотренная комбинация логических элементов получила название полусумматора. На ее вход подаются два сигнала: x₁ и х₂; выходной сигнал у дает результат сложения в том же двоичном разряде, в котором стоят складываемые числа; в случае суммирования 1 + 1 происходит перенос в старший разряд - для него имеется еще один выход b.

В арифметико-логическом устройстве компьютера полусумматор обрабатывает лишь младшие разряды регистров. Для всех остальных разрядов помимо двух складываемых значений необходимо учитывать бит переноса, образовавшийся в результате сложения предыдущих разрядов. Следовательно, комбинационная схема, обеспечивающая выполнение данной операции, должна иметь три входа (x₁, х₂ и b_i-1) и формировать два выходных значения (у и b_n) - эта схема называется двоичным сумматором. Логические функции такой схемы для каждого из разрядов i (i = 2 ... п, считая, что младшим является разряд 1):

Схема, реализующая такие логические функции - она называется последовательным двоичным сумматором - содержит 15 логических элементов (9 И, 4 ИЛИ и 2 НЕ). Схема двоичного сумматора представлена на рис. 9.3. Такой сумматор обеспечивает выполнение операций в одном из разрядов процессора. Следовательно, 32-разрядный процессор будет содержать 31 схему сумматора и1 полусумматора (для младшего разряда), которые соединены друг с другом и вместе образуют сумматор.

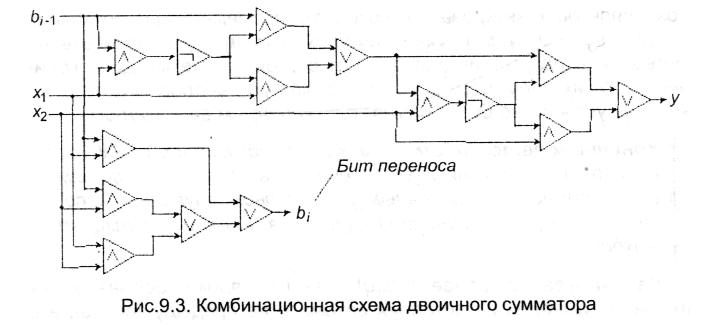
Подобным образом, вообще говоря, можно построить комбинационную схему для любого конечного множества задач, решение которых (т.е. выходные сигналы) однозначно определяются их условием (т.е. входными сигналами). В частности, если ограничиться некоторой фиксированной точностью представления числа, то можно построить комбинационную схему, которая вычисляет значение любой функции у = f(x₁,...x_n) (безусловно, в двоичных кодах), например, sin(x) и др. Однако на практике получается, что при разрядности 32 и выше даже схема умножителя, вычисляющего произведение х₁∙х₂, становится столь сложной, что оказывается проще реализовать умножение иным путем, который можно назвать алгоритмическим и который позволяет представить умножение в виде последовательности сложений и сдвигов, о чем шла речь ранее. Точно также и иные вычисления сводятся к цепочкам элементарных операций: сложение, сдвиг, инверсия и пр.