Контрольные вопросы и задания

1. Опишите формальную грамматику, порождающую множество целых двоичных чисел.

2. Измените описание грамматики из примера в п.8.1.2. таким образом, чтобы она описывала конструкции типа «Имя_1, Имя_2...Имя_N делают_то-то».

3. Что определяет следующая нотация Бекуса-Наура:

<формула>::=<цифра>|(<формула><знак><формула>)

<знак>::= +| - | *

<цифра>::= 0|1|2|3|4|5|6|7|8|9

4. На каком-либо языке программирования напишите программу, функционирующую в соответствии с нотацией, приведенной в предыдущем задании.

5. С помощью синтаксических диаграмм опишите следующие конструкции языка PASCAL:

a) оператор цикла с предусловием WHILE...DO;

b) составной оператор;

c) оператор цикла с параметром FOR...DO;

d) оператор выбора CASE.

6. Можно ли считать формальным исполнителем алгоритма следующие устройства:

a) кодовый замок;

b) графический редактор;

c) телефон с памятью для записи номеров;

d) принтер?

7. Постройте блок-схемы следующих структурных алгоритмов:

а) вычисление n! (ввод n);

b) суммирование цифр целого числа при произвольной его разрядности (ввод - целое число);

c) перевод целого числа в двоичную систему счисления (ввод - целое число);

d) вычисление значения функции sin(x) с заданной точностью е путем суммирования ее разложения в ряд Тейлора (ввод - аргумент х, точность вычисления е).

8. Запишите с помощью псевдокода алгоритмы, приведенные в задании 7.

9. Напишите программы на каком-либо языке программирования для алгоритмов задания 7.

10. В чем смысл и значение структурной теоремы для практики разработки алгоритмов? Возможно ли существование неструктурных алгоритмов? Если «да» - приведите примеры.

Глава 9. Представление о конечном автомате

Продолжаем обсуждение вопросов, связанных с обработкой (преобразованием) дискретной информации. До этого речь велась об алгоритмах, т.е. последовательности действий по преобразованию информации безотносительно того, кто (или что) эти действия будет производить. В данной главе выясним, какими качествами должны обладать технические устройства, способные производить алгоритмическую обработку дискретной информации. При этом будут рассматриваться не физическая или техническая реализация конкретных устройств, а общие принципы их строения, существенные с точки зрения обработки и хранения информации.

9.1. Общие подходы к описанию устройств, предназначенных для обработки дискретной информации

Обычно автоматом называют устройство, выполняющее без непосредственного участия человека определенную последовательность операций, в результате которой происходит преобразование материальных объектов, энергии или информации. Когда говорится «без участия человека», то подразумевается отсутствие явного управления со стороны человека в ходе выполнения операций. Однако на самом деле управление осуществляется, но опосредованно, через программу, составленную предварительно человеком и заложенную в устройство. В дальнейшем ограничим себя обсуждением лишь тех устройств, которые предназначены для автоматического преобразования информации, представленной в дискретной форме.

Поскольку устройство обменивается информацией с внешней средой, очевидно, оно должно обладать входным каналом, по которому информация поступает в него, а также выходным каналом, через который выдается результат преобразования. Помимо этого, устройство может обладать памятью, в которой фиксируется его текущее состояние; результат обработки в общем случае определяется входными воздействиями и внутренним состоянием устройства. Будем считать, что для представления входной информации используется некоторый конечный алфавит X (входной алфавит), а для представления выходной - конечный алфавит Y (выходной алфавит). Как отмечалось ранее, требование конечности алфавитов является следствием конечности времени обработки информации. Внутренние состояния устройства также образуют дискретный набор, который можно считать внутренним алфавитом - будем обозначать его Q. Что касается числа различных внутренних состояний, то пока не будем делать относительно его никаких предположений.

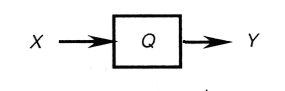
Будем считать также, что поступление входных символов и переключение состояний устройства происходят не непрерывно, а в определенные моменты времени, т.е. дискретно. Если последовательность моментов произвольна, то говорят об асинхронной организации работы элементов устройства, например, набор номера телефона или кода замка. Однако в сложных устройствах чаще используется синхронная организация, при которой моменты поступления и выхода сигналов, а также переключения внутренних состояний следуют друг за другом через один и тот же фиксированный промежуток времени ∆t = const, называемый тактом. Эти моменты задаются с помощью специального устройства - тактового генератора (или генератора синхроимпульсов). Число тактовых импульсов за единицу времени называется тактовой частотой - она является одним из важнейших факторов, определяющих быстродействие устройства. Можно ввести моменты времени t₀, t₁, t₂,..., обозначающие границы тактов (t₀ соответствует моменту начала работы). При этом можно считать, что события, относящиеся к такту i - поступление входного символа, изменение внутреннего состояния, формирование и выдача выходного символа - проистекают мгновенно в момент t_i.

Устройства, у которых дискретны множества внутренних состояний, входных и выходных сигналов, а также множество моментов времени, в которые поступают входные сигналы, меняются внутренние состояния и выдаются выходные сигналы, называются дискретными.

Примерами дискретных устройств являются наборный диск телефона, кодовый замок, калькулятор, электронные табло и, безусловно, компьютер. По назначению устройства можно объединить в три группы:

• информационные - справочные автоматы, электронные табло, светофоры, устройства аварийной сигнализации и пр.;

• управляющие - кодовый замок, устройство управления лифтом, станки с программным управлением, микропроцессоры фотоаппарата, видео и пр.;

• вычислительные - микрокалькулятор, микропроцессоры компьютеров.

Существуют устройства, осуществляющие деятельность всех трех видов, например, компьютер, автопилот и др.

Для наших рассуждений существенным оказывается то обстоятельство, что символы на выходе и внутренние состояния такого устройства оказываются дискретными функциями входных символов и номеров тактов работы. Введем понятие функции переходов , которая будет связывать внутреннее состояние устройства на последующем такте с состоянием и входным символом на текущем такте:

Другими словами, функция переходов показывает, в какое состояние из всех возможных Q перейдет дискретное устройство, если оно находилось в состоянии q_i, а на вход поступил символ x_i.

Подобным же образом введем функцию выходов , которая будет связывать внутреннее состояние устройства и входной символ на текущем такте с выходным сигналом на этом же такте:

Следовательно, функция выходов определяет, какой символ образуется на выходе, если на данном такте определен символ на входе и состояние устройства.

Говорят, что пятеркой компонентов <Х, Y, Q, Ψ, Θ> задается автомат, обеспечивающий преобразование по определенным правилам последовательностей символов входного алфавита в выходную последовательность. Действительно, если принять начальное условие q₁ = q₀, то рекуррентные соотношения (9.1) и (9.2) определят порядок преобразования конечной последовательности входных символов x₀, x₁ ..., x_n в некоторую последовательность выходных символов той же длины у₀, y₁,....y_n; при этом будет возникать определенная последовательность внутренних состояний q₁, q₂, ... . В этом и заключается функционирование автомата. Выходной символ, вырабатываемый автоматом на некотором такте i, зависит не только от входного символа, воспринятого на этом же такте, но и от символов, поступивших ранее - они фиксируются в автомате путем изменения его внутреннего состояния. В этом смысле множество внутренних состояний автомата является его внутренней памятью. В зависимости от объема этой памяти выделяются следующие типы автоматов:

• без памяти;

• с конечной памятью;

• с бесконечной памятью.

Забегая несколько вперед, заметим, что автомат с конечной памятью называется конечным автоматом. Отметим также, что функции переходов и выходов имеют обобщающее название автоматные функции.

Что касается дискретных устройств с бесконечной памятью -это чисто модельное теоретическое представление, поскольку никакие реальные устройства бесконечной памятью обладать не могут. Примером автомата с бесконечной памятью может служить машина Тьюринга, в которой, как указывалось в п. 7.3.3, роль памяти выполняет бесконечная (или при необходимости наращиваемая) в обе стороны бумажная лента. Таким образом, можно считать, что автоматом с бесконечной памятью является алгоритм, представленный в форме машины Тьюринга. Поскольку вопросы, связанные с функционированием машин Тьюринга уже рассматривались ранее, в данной главе они обсуждаться не будут.

В реальных дискретных устройствах сигналы и их преобразования могут иметь различную физическую природу (электрическую, механическую, пневматическую и пр.). Однако от этой природы можно отвлечься и изучать только общие законы построения автоматов и правила, определяющие преобразование информации ими. Такие автоматы называются абстрактными. В теории абстрактных автоматов решаются несколько групп проблем:

во-первых, выясняется, какие преобразования возможны в автомате, как их описать, как выполняемые преобразования связаны с числом состояний (т.е. сложностью) автомата, существуют ли неразрешимые автоматом задачи;

во-вторых, исследуются эквивалентные преобразования автоматов; задача эквивалентного преобразования состоит в построении автомата эквивалентного данному, но имеющего иное количество состояний (обычно, меньшее);

в-третьих, рассматривается круг вопросов, в которых определяется строение автомата по характеру и соотношению входных и выходных сигналов (автомат - «черный ящик») - это важная прикладная задача технической диагностики устройств, без которой невозможна их практическая эксплуатация;

в-четвертых, выделяются структурных элементов автоматов и определяются правил построения из них сложных устройств (задача синтеза автоматов) - с этим связана разработка новых автоматов, в частности, компьютеров.

Важным для практики частным случаем являются автоматы, в которых вся информация представлена с помощью двоичного кода, т.е. алфавиты X, Y и Q являются двоичными - такие автоматы называют двоичными или логическими. Последнее название обусловлено тем, что, как показывает теория, при двоичном кодировании любой конечный автомат можно представить в виде комбинации некоторого числа элементов, реализующих логические операции И, ИЛИ, НЕ, а также элементы памяти (задержка и триггер). Объединение элементов называется логической схемой. Важными представляются два обстоятельства: во-первых, работу логических схем можно описать законами и правилами математической логики (т.е. результат действия логической схемы сводится к вычислению значения логического выражения); во-вторых, из данного небольшого набора элементов можно построить любой конечный автомат.