8.1.2. Способы описания формальных языков

Как уже было сказано, для описания языка-объекта должен применяться метаязык. Но метаязык также должен обладать некоторыми свойствами формального языка, чтобы однозначно определять конструкции языка-объекта. Следовательно, метаязык должен быть сначала описан сам, для чего также нужен язык - естественно, может сложиться впечатление, что такой процесс никогда не закончится. Однако доказано, что для описания любого метаязыка можно использовать язык естественный. Таким образом, для построения формального языка необходимо средствами естественного языка описать метаязык, а затем посредством метаязыка описать язык формальный. Рассмотрим два варианта описания метаязыков.

Один из широко распространенных метаязыков известен как нотации Бекуса-Наура. Для формирования предложений в форме Бекуса-Наура используются универсальные метасимволы: { <, >, ::=, | }. Первые два метасимвола называют «угловыми скобками» - они служат для обрамления нетерминального символа. Символ «::=» читается «по определению есть»; символ «|» - «или». В предложениях, записанных в форме Бекуса-Наура, нетерминальный символ, стоящий в угловых скобках, играет роль определяемой конструкции языка-объекта. В формулах Бекуса-Наура могут использоваться терминальные символы из алфавита языка-объекта, отличные от универсальных метасимволов. Терминальные символы формального языка ничем не ограничиваются.

Описание формального языка строится из последовательности формул, каждая из которых в левой части содержит один метасимвол, обозначающий некоторую конструкцию языка-объекта. Правая часть такой формулы содержит либо перечисление метасимволов и терминальных символов языка-объекта (никаких разделителей при этом не ставится), либо совокупности перечислений, разделенных символом «|». Правая и левая части объединяются в единую формулу знаком «::=».

Язык-объект можно считать полностью определенным в форме Бекуса-Наура, если любой нетерминальный символ можно представить последовательностью терминальных символов.

В качестве примера можно рассмотреть определение понятия «идентификатор», которое используется во многих языках программирования. На естественном языке определение звучит следующим образом: «Идентификатор - это любая последовательность букв и цифр, начинающаяся с буквы». В форме Бекуса-Наура оно будет выглядеть следующим образом:

<идентификатор>::=<буква>/<идентификатор>< буква> /<идентификатор>

Видно, что в определении данного понятия присутствует рекурсивность, поскольку понятие «идентификатор» определяется через само себя. Элементарным оказывается идентификатор из одной буквы.

Достоинство нотаций Бекуса-Наура в том, что они представляется в буквенном виде; неудобны нотации однообразностью способов построения предложений языка-объекта - запись оказывается громоздкой и плохо воспринимаемой.

Гораздо более наглядной следует считать другой способ описания формального языка, предложеннный Никласом Виртом - создателем языка программирования PASCAL, получивший название «синтаксические диаграммы». Синтаксическая диаграмма - это схема (графическое представление) описания какого-либо нетерминального символа языка-объекта. Схема всегда имеет один вход и один выход. Элементами схемы могут служить терминальные символы языка-объекта, заключенные в окружность (или овал) или нетерминальные символы (понятия) языка-объекта, заключенные в прямоугольник. Элементы соединяются между собой направленными линиями, указывающие порядок следования объектов в определяемом нетерминальном символе.

Структура синтаксических диаграмм идентична структурам языков программирования, что позволило широко использовать диаграммы для написания трансляторов различных языков. Первым языком, описанным с помощью синтаксических диаграмм, был язык PASCAL.

Чтение диаграммы производится в направлении стрелок; в точке ветвления может выбираться любой маршрут. В качестве метаязыка может использоваться естественный русский язык; языки программирования строятся на англоязычной основе. Терминальные символы переписываются в конструкции формального языка дословно. Нетерминальные символы могут выражаться через терминальные или другие нетерминальные - в этом случае для них строятся уточняющие диаграммы; в конечном счете, все нетерминальные символы должны быть выражены через терминальные. При использовании синтаксических диаграмм принимается условие, что среди терминальных символов языка-объекта не должно быть одинаковых, а также ни один из терминальных символов не может служить началом другого. При нарушении данного условия возможно неоднозначное чтение диаграммы и, как следствие, построение или распознавание неверной конструкции языка.

Рассмотрим ряд примеров построения синтаксических диаграмм, первым из которых будет определение понятия «Идентификатор» для сопоставления с приведенной выше нотацией Бекуса-Наура.

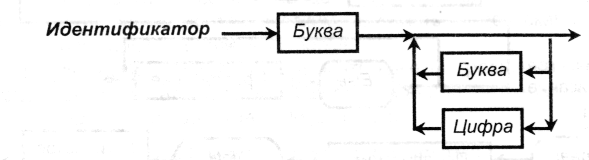
Необходимы уточняющими диаграммы:

Примерами построения англоязычных идентификаторов в соответствии с этой диаграммой являются: q, a 123, identificator, e2e4.

Диаграмма, задающая общий вид программы на языке PASCAL, выглядит следующим образом:

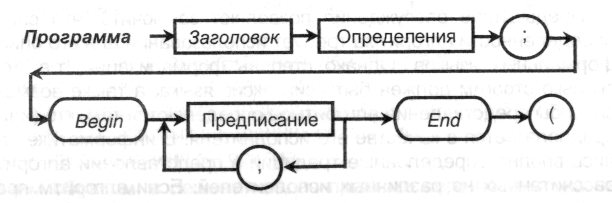
В качестве примеров предписаний рассмотрим условное и циклическое.

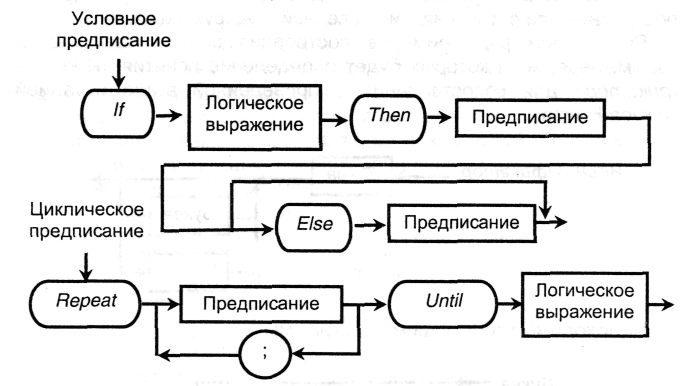
В соответствии с этими и подобными диаграммами строятся допустимые синтаксические конструкции языка.

Итак, нотации Бекуса-Наура и синтаксические диаграммы - это два альтернативных способа описания конструкций метаязыка, с помощью которого строится формальный язык. После того, как построена формальная грамматика, и ею порожден язык, он может быть использован для решения прикладных задач - коммуникации, хранения и обработки информации. Последний класс задач приводит к необходимости формулировки с помощью языков последовательностей обработки информации, т.е. алгоритмов, и их представлению в форме, доступной для понимания и исполнения лицом или техническим устройством, которые обработку производят.