Глава 8. Формализация представления алгоритмов
Абстрактные алгоритмические модели, как уже неоднократно отмечалось, используются лишь при построении теории и доказательстве общих свойств алгоритмов. Для практических целей такое представление алгоритмов чаще всего неудобно, поскольку, во-первых, не всегда практически реализуема форма представления (например, машина Тьюринга или Поста); во-вторых, элементарные шаги, выделяемые в моделях, оказываются слишком «мелкими» для современных технических устройств, которые выступают в качестве исполнителей алгоритмов. В связи с этим встает вопрос о том, как может быть описан алгоритм, предназначенный для решения практической задачи с помощью реального технического устройства? Обсуждению вариантов ответа на него и посвящена данная глава.
8.1. Формальные языки
8.1.1. Формальная грамматика
Алгоритм был ранее определен как алфавитный оператор с конечной системой правил преобразования. Для записи входных, промежуточных и выходных слов используется некоторый алфавит. Каким-то образом должны быть описаны и правила преобразования. Очевидно, для этого требуется некоторый язык. Пригоден ли для описания алгоритма обычный разговорный язык?
Любой естественный язык возникал как средство общения людей. Именно по этой причине ему присущи такие особенности как:
изменчивость, которая состоит в непостоянстве словарного состава языка;
неоднозначность трактовки фраз различными людьми;
избыточность, о чем шла речь в главе «Кодирование символьной информации».
Перечисленные особенности не позволяют применить естественный язык для записи алгоритма, поскольку одним из свойств алгоритма является его детерминированность, т.е. однозначность выполнения шагов любым исполнителем. Наиболее простой путь преодоления нежелательных свойств естественных языков - построение языков искусственных со строгим синтаксисом и полной смысловой определенностью - такие языки получили название формальных.
В любом языке - естественном или искусственном - можно выделить две составляющие: синтаксис и семантику. Синтаксис (грамматика языка) - это совокупность правил, согласно которым строятся допустимые в данном языке конструкции. Семантика -смысловая сторона языка - она соотносит единицы и конструкции языка с некоторым внешним миром, для описания которого язык используется.
Для описания формального языка необходим другой язык, с помощью которого будут создаваться языковые конструкции. Описываемый формальный язык называется языком-объектом, а язык, средствами которого производится описание - метаязыком. Метаязык должен обеспечивать как описание структурных единиц языка и правил объединения их в допустимые предложения, так и содержательную (смысловую) сторону языковых конструкций.
Любая грамматика начинается с указания алфавита, т.е. набора символов, посредством которого строятся конструкции языка.
Синтаксис формального языка задается некоторой системой правил (порождающей системой), которая из небольшого набора исходных конструкций порождает все допустимые их комбинации, т.е. язык образуется как множество разрешенных правилами сочетаний исходных конструкций. Кроме этого, синтаксис содержит формулировку условия, которое выполняется для законченных конструкций языка и не выполняется в противном случае.
Помимо синтаксиса устанавливается система правил, позволяющих конструкциям языка придать смысл - эти правила образуют семантику языка.
Формальная грамматика - система правил, описывающая множество конечных последовательностей символов формального алфавита.
Конечные цепочки символов называются предложениями формального языка, а само множество цепочек - языком, описываемым данной грамматикой.
Набор синтаксических правил формального языка аналогичен системе подстановок, используемых в нормальных алгоритмах Маркова. Вывод в данной порождающей грамматике есть последовательность цепочек, в которой любая, начиная со второй, получается из предыдущей применением какого-либо правила вывода.
Формальная грамматика задается упорядоченной четверкой {T, N, S, Р}, где Т и N - непересекающиеся конечные множества, образующие алфавит или словарь порождаемого формального языка; Т называется множеством (словарем) терминальных символов; N - множеством (словарем) нетерминальных (вспомогательных) символов. S - начальный (выделенный) вспомогательный символ из множества N. Р - набор правил вывода конструкций языка (подстановок) из выделенного вспомогательного символа, имеющие вид g→ h, где g и h - цепочки, состоящие как из терминальных, так и нетерминальных символов.
Подстановки работают следующим образом: если в преобразуемой цепочке есть слово g, то оно заменяется словом h. Единственное ограничение на вид подстановок состоит в том, что слово g не может состоять только из терминальных символов. Это означает, что получение на некотором шаге цепочки, состоящей только из терминальных символов, свидетельствует о прекращении процесса порождения - эта цепочка является правильной, завершенной конструкцией порождаемого языка. Подстановки Р могут применяться к трансформируемой цепочке в произвольном порядке.
Пример 8.1
Пусть формальная грамматика задается следующим образом: T = {а, b} (т.е. множество терминальных символов - алфавит языка - состоит из двух символов - а и b); N = {S}, т.е. множество нетерминальных символов состоит из единственного символа S - он, естественно, оказывается выделенным; система подстановок пусть имеет следующий вид: S→ aSa, S→ bSb, S→ a, S→ b
Описанная грамматика порождает язык, состоящий из всех «слов-перевертышей» в алфавите {а, b}, имеющих нечетную длину, т.е. слов, которые слева направо читаются также, как справа налево, например, aba, abababa, bbbbb, baaaaaab и т.д. Легко видеть, что применение первых двух правил (в любом числе и любой последовательности) порождает цепочки (слова) типа αSα-1, где α-1 означает слово α, записанное справа налево; применение третьего и четвертого правил завершает процесс порождения слова и формируют слова типа αаα-1 или αbα-1 .
Пример 8.2
Рассмотрим формальную грамматику, порождающую фрагмент естественного языка. Пусть Т = {а, б, ...я, А, Б, ...Я} - множество терминальных символов - букв русского алфавита. Нетерминальный алфавит строится из символов N = {Q, R, S}, где Q = {q1,...qn} - множество имен людей в русском алфавите, R = {r1,...rm} - множество глаголов, стоящих в третьем лице единственного числа настоящего времени, ri и qj записываются с помощью терминальных символов. Пусть система подстановок имеет вид:
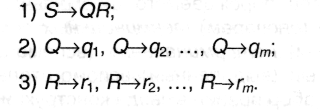
Очевидно, эта грамматика порождает язык, состоящий из фраз типа: «такой-то делает то-то», например, «Маша читает», «Вася спит» и т.п. Работает грамматика следующим образом: на первом шаге определяется тип фразы; второй шаг порождает конкретное имя, а третий шаг - конкретное действие (глагол). Из данного примера виден содержательный смысл нетерминальных символов - они могут обозначать различные классы конкретных слов, в частности, традиционные грамматические классы - части речи, члены предложения и пр.
Подойдя к рассмотрению формальных грамматик в связи с необходимостью построения строгого (однозначно понимаемого) описания алгоритма, отметим, что на самом деле области их применения в информатике гораздо обширнее. На основе формальных грамматик создаются языки программирования и трансляторы к ним. При решении задач искусственного интеллекта они используются в системах машинного перевода, а также для генерации синтаксически правильных предложений в ответах экспертных систем на запросы пользователей. Формальные грамматики могут быть применяться в учебных и иных программах (например, Microsoft Word), где требуется проверка правильности вводимого текста и поиск в нем ошибок.