1.2. Формы представления информации
В предыдущем пункте было сказано, что передача информации производится с помощью сигналов, а самим сигналом является изменение некоторой характеристики носителя с течением времени. При этом в зависимости от особенностей изменения этой характеристики (т.е. параметра сигнала) с течением времени выделяют два типа сигналов: непрерывные и дискретные.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.
Если обозначить Z - значение параметра сигнала, a t - время, то зависимость 2(1) будет непрерывной функцией (рис.1.1,а).
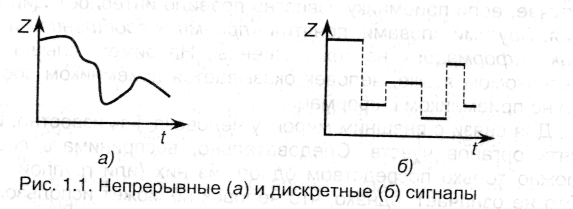
Примерами непрерывных сигналов являются речь и музыка, изображение, показание термометра (параметр сигнала - высота столба спирта или ртути - имеет непрерывный ряд значений) и пр.
Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.
Пример дискретных сигналов представлен на рис. 1.1,б. Как следует из определения, дискретные сигналы могут быть описаны дискретным и конечным множеством значений параметров {Z}. Примерами устройств, использующих дискретные сигналы, являются часы (электронные и механические), цифровые измерительные приборы, книги, табло и пр.
Поскольку последовательность сигналов есть сообщение, качество прерывности-непрерывности сигналов переносится и на сообщение - существуют понятия «непрерывное сообщение» и «дискретное сообщение». Очевидно, что дискретным будет считаться сообщение, построенное из дискретных сигналов. Гораздо меньше оснований приписывать данное качество самой информации, поскольку информация - категория нематериальная и не может обладать свойством дискретности или непрерывности. С другой стороны, одна и та же информация, как уже было сказано, может быть представлена посредством различных сообщений, в том числе и отличающихся характером сигналов. Например, речь, которую слышим, можно записать в аналоговом виде с помощью магнитофона, а можно и законспектировать посредством дискретного набора букв. По этой причине в информатике существуют и используются сочетания «непрерывная информация» и «дискретная информация». Их нужно понимать только как сокращение полных фраз: «информация, представленная посредством непрерывных сигналов» и «информация, представленная посредством дискретных сигналов» - именно в таком контексте эти понятия будут использоваться в дальнейшем изложении. Поэтому когда заходит речь о видах информации, правильнее говорить о формах ее представления в сообщении или о видах сообщений.
Принципиальным и важнейшим различием непрерывных и дискретных сигналов является то, что дискретные сигналы можно обозначить, т.е. приписать каждому из конечного чисел возможные значения сигнала знак, который будет отличать данный сигнал от другого
Знак - это элемент некоторого конечного* множества отличных друг от друга сущностей.
* Теоретически можно было бы обойтись без требования конечности, однако, это не имело бы никакого практического значения, поскольку за конечное время всегда можно передать только сообщения, построенные из конечного числа знаков.
Природа знака может любой - жест, рисунок, буква, сигнал светофора, определенный звук и т.д. Природа знака определяется носителем сообщения и формой представления информации в сообщении.
Вся совокупность знаков, используемых для представления дискретной информации, называется набором знаков. Таким образом , набор есть дискретное множество знаков.
Набор знаков, в котором установлен порядок их следования, называется алфавитом.
Следовательно, алфавит - это упорядоченная совокупность знаков. Порядок следования знаков в алфавите называется лексикографическим. Благодаря этому порядку между знаками устанавливаются отношения «больше-меньше»: для двух знаков ξ и ψ принимается, что ξ < ψ, если порядковый номер у ξ в алфавите меньше, чем у ψ.
Примером алфавита может служить совокупность арабских цифр 0,1...9 - с его помощью можно записать любое целое число в системах счисления от двоичной до десятичной. Если к этому алфавиту добавить знаки «+» и «-», то сформируется набор знаков, применимый для записи любого целого числа, как положительного, так и отрицательного; правда, этот набор нельзя считать алфавитом, поскольку в нем не определен порядок следования знаков.. Наконец, если добавить знак разделителя разрядов («.» или «,»), то такой алфавит позволит записать любое вещественное число.
Поскольку при передаче сообщения параметр сигнала должен меняться, очевидно, что минимальное количество различных его значений равно двум и, следовательно, алфавит содержит минимум два знака - такой алфавит называется двоичным. Верхней границы числа знаков в алфавите не существует; примером могут служить иероглифы, каждый из которых обозначает целое понятие, и общее их количество исчисляется десятками тысяч.
Знаки, используемые для обозначения фонем человеческого языка, называются буквами, а их совокупность - алфавитом языка.
Сами по себе знак или буква не несут никакого смыслового содержания. Однако такое содержание им может быть приписано - в этом случае знак будет называться символом. Например, массу в физике принято обозначать буквой т - следовательно, т является символом физической величины «масса» в формулах. Другим примером символов могут служить пиктограммы, обозначающие в компьютерных программах объекты или действия.
Таким образом, понятия «знак», «буква» и «символ» нельзя считать тождественными, хотя весьма часто различия между ними не проводят, поэтому в информатике существуют понятия «символьная переменная», «кодировка символов алфавита», «символьная информация» - во всех приведенных примерах вместо термина «символьный» корректнее было бы использовать «знаковый» или «буквенный».
Представляется важным еще раз подчеркнуть, что понятия знака и алфавита можно отнести только к дискретным сообщениям.