5.4.2. Коды, обнаруживающие ошибку

Задача обнаружения ошибки может быть решена довольно легко. Достаточно просто передавать каждую букву сообщения дважды. Например, при необходимости передачи слова «гора» можно передать «ггоорраа». При получении искаженного сообщения, например, «гготрраа» с большой вероятностью можно догадаться, каким было исходное слово. Конечно, возможно такое искажение, которое делает неоднозначным интерпретацию полученного сообщения, например, «гпоорраа», «ггоорреа» или «кгоорраа». Однако цель такого способа кодирования состоит не в исправлении ошибки, а в фиксации факта искажения и повторной передаче части сообщения в этом случае. Недостаток данного способа обеспечения надежности состоит в том, что избыточность сообщения оказывается очень большой - очевидно, L = 2.

Поскольку ошибка должна быть только обнаружена, можно предложить другой способ кодирования. Пусть имеется цепочка информационных бит длиной k_i. Добавим к ним один контрольный бит (k_c = 1), значение которого определяется тем, что новая кодовая цепочка из k_i + 1 бит должна содержать четное количество единиц - по этой причине такой контрольный бит называется битом четности. Например, для информационного байта 01010100 бит четности будет иметь значение 1, а для байта 11011011 бит четности равен 0. В случае одиночной ошибки передачи число 1 перестает быть четным, что и служит свидетельством сбоя. Например, если получена цепочка 110110111 (контрольный бит выделен подчеркиванием), ясно, что передача произведена с ошибкой, поскольку общее количество единиц равно 7, т.е. нечетно. Предложенный способ кодирования не позволяет установить, в каком конкретно бите содержится ошибка и, следовательно, не дает возможности ее исправить. Избыточность сообщения при этом равна:

На первый взгляд кажется, что путем увеличения k_i можно сколь угодно приближать избыточность к ее минимальному значению (L_min = 1). Однако с ростом k_i, во-первых, растет вероятность парной ошибки, которая контрольным битом не отслеживается; во-вторых, при обнаружении ошибки потребуется заново передавать много информации. Поэтому обычно k_i = 8 или 16 и, следовательно, L = 1,125 (1,0625).

5.4.3. Коды, исправляющие одиночную ошибку

По аналогии с предыдущим пунктом можно было бы предложить простой способ установления ошибки - передавать каждый символ трижды, например, «гггооорррааа» - тогда при получении сообщения «гггооопррааа» ясно, что ошибочной оказывается буква «л» и ее следует заменить на «р». Безусловно, при этом предполагается, что вероятность появления парной ошибки невелика. Такой метод кодирования приводит к избыточности сообщения L = 3, что неприемлемо с экономической точки зрения.

Прежде, чем обсуждать метод кодирования, позволяющий локализовать и исправить ошибку передачи, произведем некоторые количественные оценки. Как показано в п.5.3, наличие шумов в канале связи ведет к частичной потере передаваемой информации на величину возникающей неопределенности, которая при передаче одного бита исходного сообщения составляет

где р - вероятность появления ошибки в сообщении. Для восстановления информационного содержания сообщения, очевидно, следует дополнительно передать количество информации не менее величины ее потерь, т.е. вместо передачи каждого 1 бит информации следует передавать 1 + Н, бит. В этом случае избыточность сообщения составит

Приведенную избыточность следует считать минимальной (это указывает ее индекс), поскольку при передаче сообщения по каналу, характеризуемому вероятностью искажения р, при избыточности, меньшей L_min восстановление информации оказывается невозможным.

Пример 5.3

Какое минимальное количество контрольных бит должно передаваться вместе с 16-ю информационными для обеспечения восстановимости информации, если вероятность искажения составляет 1%?

Подставляя р = 0,01 в (5.7), находим L_min  1,081. При k_i = 16 из (5.6.) получаем k = k_i ∙ L_min = 17,29. Следовательно, с учетом того, что количество контрольных бит выражается целым числом, k_c ≥ k - k_i = 2. Реальная избыточность согласно (5.6) составит L = 1,125.

Выражение (5.7) устанавливает границу избыточности, при которой возможно восстановление переданной информации, однако, не указывает, каким образом следует осуществить кодирование, чтобы ошибка могла быть локализована (т.е. определено, в каком бите она находится) и, естественно, устранена. Такой метод кодирования был предложен в 1948 г. Р. Хеммингом; построенные по этому методы коды получили название коды Хемминга [36].

Основная идея состоит в добавлении к информационным битам нескольких битов четности, каждый из которых контролирует определенные информационные биты. Если пронумеровать все передаваемые биты, начиная с 1 слева направо (стоит напомнить, что информационные биты нумеруются с 0 и справа налево), то контрольными (проверочными) оказываются биты, номера которых равны степеням числа 2, а все остальные являются информационными. Например, для 8-битного информационного кода контрольными окажутся биты с номерами 1, 2, 4 и 8:

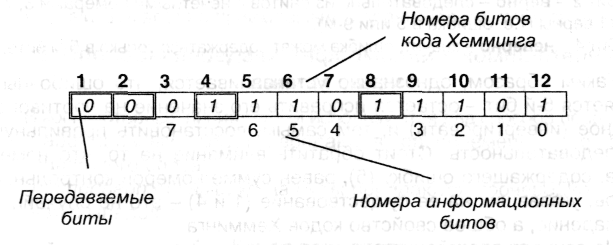
Номера контролируемых битов для каждого проверочного приведены в табл. 5.1. В перечень контролируемых битов входит и тот, в котором располагается проверочный. При этом состояние проверочного бита устанавливается таким образом, чтобы суммарное количество единиц в контролируемых им битах было бы четным.

Таблица 5.1.

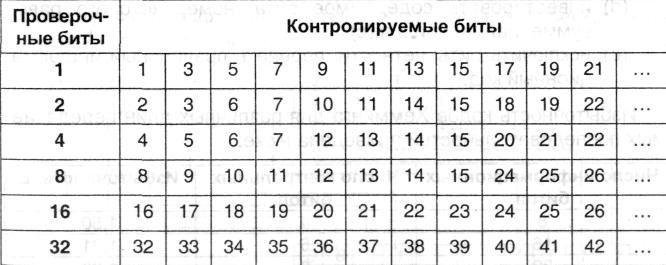
Легко усматривается принцип выделения контролируемых битов в табл. 5.1: для любого номера проверочного бита (п), начиная с него, п бит подряд оказываются проверяемыми, затем - группа п непроверяемых бит; далее происходит чередование групп.

Пример 5.4

Пусть вместо указанной выше последовательности 000111011101 пришла следующая (в 5-м бите 1 заменилась 0):

Анализируем состояния контрольных битов в соответствии с табл. 5.1.

Бит 1 - неверно - т.е. ошибка находится в каком-либо бите с нечетным номером.

Бит 2 - верно - следовательно из байтов с нечетными номерами 3, 7 и 11 верны (т.е. ошибка в 5 или 9-м).

Бит 4 - неверно - значит, ошибка может содержаться только в 5-м бите.

Таким образом, однозначно устанавливается, что ошибочным является 5-й бит - остается исправить его значение на противоположное (инвертировать) и, тем самым, восстановить правильную последовательность. Стоит обратить внимание на то, что номер бита, содержащего ошибку (5), равен сумме номеров контрольных битов, указавших на ее существование (1 и 4) - это не случайное совпадение, а общее свойство кодов Хемминга.

На основании сказанного можно сформулировать простой алгоритм проверки и исправления передаваемой последовательности бит в представлении Хемминга:

(a) произвести проверку всех битов четности;

(b) если все биты четности верны, то перейти к п.(е);

(c) вычислить сумму номеров всех неправильных битов четности;

(d) инвертировать содержимое бита, номер которого равен сумме, найденной в п.(с);

(e) исключить биты четности, передать правильный информационный код.

Избыточность кодов Хемминга для различных длин передаваемых последовательностей приведена ниже:

Из сопоставления видно, что выгоднее передавать и хранить более длинные последовательности битов. При этом, однако, избыточность не должна оказаться меньше L_min для выбранного канала связи.

Безусловно, данный способ кодирования требует увеличения объема памяти компьютера приблизительно на одну треть при 16-битной длине машинного слова, однако, он позволяет автоматически исправлять одиночные ошибки. Поэтому, оценивая время наработки на отказ, следует исходить из вероятности появления парной ошибки в одной последовательности (т.е. сбои должны произойти в двух битах одновременно). Расчеты показывают, что для указанного ранее количества ячеек в памяти объемом 1 Мбайт среднее время появления ошибки составляет более 80 лет, что, безусловно, можно считать вполне приемлемым с практической точки зрения.