5.3. Влияние шумов на пропускную способность канала

Как показано в теории Шеннона, утверждение, сформулированное в конце предыдущего пункта, справедливо как при отсутствии в канале помех (шумов) (идеальный канал связи), так и при их наличии (реальный канал связи). Отличие реального канала от идеального в том, что шумы приводят к снижению пропускной способности канала. Покажем это для частного случая использования двух элементарных сигналов равной длительности. Каждый из них на входе канала связи несет I_imp = 1 бит информации. После прохождения сигнала по идеальному каналу и на выходе импульс (1) интерпретируется именно как импульс, а пауза (0) - как пауза и, следовательно, связанная с ними информация не меняется в количественном отношении. Иная ситуация в реальном канале: из-за шумов при передаче может произойти искажение сигнала, в результате чего вместо 1 на выходе будет получен 0, а вместо 0 - 1. Пусть вероятности таких искажений для 0 и 1 одинаковы, т.е. p_1→0 = p_0→1 = р. Тогда вероятность того, что исходный сигнал придет без искажений, очевидно, равна 1 - р. Следовательно, при интерпретации (распознавании) конечного сигнала возникает неопределенность, которая, как следует из формул (2.4) и (А.8), может быть охарактеризована средней энтропией:

Эта неопределенность приведет к уменьшению количества информации, содержащейся в сигнале, на величину Н, т.е.

Поскольку длительность импульса τ₀ определяется частотой v_m и не зависит от наличия шумов, пропускная способность реального канала С_R оказывается меньше, чем аналогичного идеального С:

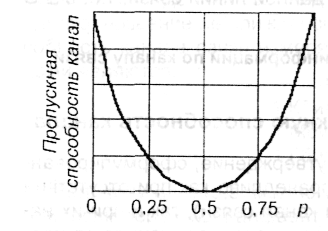
На графике показана зависимость С_R(р). Как следует из (5.5), при р = 0,5 (I_iтр)' = 0 и, следовательно, С_R = 0. Это связано с тем, что в данном случае на приемном конце линии связи с одинаковой вероятностью получаются 0 и 1 независимо от того, каков был сигнал на входе, так что передача информации по такой линии оказывается вообще невозможной. Максимального значения пропускная способность достигает при р = 0, что соответствует отсутствию помех, а также при р = 1, т.е. таких помехах, которые каждый входной сигнал 1 переводят в 0 на выходе, а каждый 0 на входе - в 1 на выходе -ясно, что помехи такого рода не мешают распознаванию того, какой сигнал был послан и, следовательно, пропускная способность от этого не страдает. В остальных случаях С < Ср.

Пример 5.2

Каково отношение С_R/С, если средняя частота появления ошибки при передаче сообщения по линии связи с шумом составляет 1 ошибочный знак на 100 переданных, если используется двоичное кодирование? Очевидно, вероятность появления ошибки передачи р = 1/100; поскольку код двоичный, I_imp = 1 бит. Следовательно, из (5.3) и (5.5) получаем:

т.е. пропускная способность канала снизилась приблизительно на 8%.

Влияние шумов определяется соотношением мощности сигнала и мощности помех. Например, для так называемого белого гауссова шума, в котором помехи существуют на всех частотах, а их амплитуды подчиняются нормальному (гауссову) распределению:

где N_s - средняя мощность сигнала, a N_n - средняя мощность помех. Из этого соотношения, в частности, видно, что для увеличения пропускной способности канала связи необходимо увеличивать полосу пропускания, либо улучшать отношение мощности сигнала к мощности помех.

Приведем характеристики некоторых каналов связи*.

* Данные взяты из книги Ф. Бауэра и Г. Гооза [4, с.65-66].

Из сопоставления данных видно, что пропускная способность телефонного канала связи совпадает с пропускной способностью органов слуха человека. Однако она существенно выше скорости обработки информации человеком, которая составляет не более 50 бит/с. Другими словами, человеческие каналы связи допускают значительную избыточность информации, поступающей в мозг.

Таким образом, наличие помех (шумов) в канале связи приводит не только к искажению передаваемого сообщения и частичной утраты связанной с ним информации, но и к уменьшению пропускной способности канала.