5.2. Характеристики канала связи

Ограничим дальнейшее рассмотрение каналами связи, передача сообщений по которым осуществляется за счет электрических импульсов - с практической точки зрения, а также для компьютерных линий связи эти каналы представляют наибольший интерес.

Ширина полосы пропускания

Любой преобразователь, работа которого основана на использовании колебаний (электрических или механических) может формировать и пропускать сигналы из ограниченной области частот. Пример с телефонной связью приводился выше. То же следует отнести и к радио и телевизионной связи - весь частотный спектр разделен на диапазоны (ДВ, СВ, KBI, КВII, УКВ, ДМВ), в пределах которых каждая станция занимает свой поддиапазон, чтобы не мешать вещанию других.

Интервал частот, используемый данным каналом связи для передачи сигналов, называется шириной полосы пропускания.

Для построения теории важна не сама ширина полосы пропускания, а максимальное значение частоты из данной полосы (v_m), поскольку именно ей определяется возможная скорость передачи информации по каналу.

Длительность элементарного импульса может быть определена из следующих соображений. Если параметр сигнала меняется синусоидально, то, как видно из рисунка, за один период колебания Т сигнал будет иметь одно максимальное значение и одно минимальное.

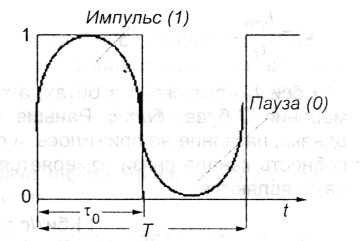
Если аппроксимировать синусоиду прямоугольными импульсами и сместить начало отсчета на уровень минимального значения, получатся, что сигнал принимает всего два значения - максимальное (обозначим его «1») - импульс, и минимальное (можно обозначить «0») - пауза. Импульс и паузу можно считать элементарными сигналами; при выбранной аппроксимации их длительности, очевидно одинаковы и равны:

Если же импульсы порождаются тактовым генератором, имеющим частоту v_m, то

Таким образом, каждые τ₀ секунд можно передавать импульс или паузу, связывая с их последовательностью определенные коды. Использовать сигналы большей длительности, чем τ₀, в принципе, возможно (например, 2τ₀) - это не приведет к потере информации, хотя снизит скорость ее передачи по каналу. Использование же сигналов более коротких, чем τ₀, может привести к информационным потерям, поскольку сигналы тогда будут принимать какие-то промежуточные значения между минимальным и максимальным, что затруднит их интерпретацию.

Таким образом, v_m определяет длительность элементарного сигнала τ₀, используемого для передачи сообщения.

Пропускная способность канала связи

Если с передачей одного импульса связано количество информации I_iтр: а передается оно за время τ₀, отношение Ii_тр к τ₀, очевидно, будет отражать среднее количество информации, передаваемое по каналу за единицу времени - эта величина является характеристикой канала связи и называется пропускной способностью канала С:

Если I_iтр выражено в битах, а τ₀ - в секундах, то единицей измерения С будет бит/с. Раньше такая единица называлась бод, однако, название не прижилось, и по этой причине пропускная способность канала связи измеряется в бит/с. Производными единицами являются:

Величину I_imp в (5.3) можно установить из следующих соображений: если первичный алфавит содержит N знаков с вероятностями появления их в сообщении р_i, то по формуле Шеннона (2.17) можно найти среднюю информацию на знак первичного алфавита I₁, для представления которого используется двоичный код длиной К⁽²⁾, то, очевидно,

При подстановке в (5.3) получаем:

Пример 5.1

Первичный алфавит состоит из трех знаков с вероятностями p₁ = 0,2; р₂ = 0,7; р₃ = 0,1. Для передачи по каналу без помех используются равномерный двоичный код. Частота тактового генератора 500 Гц.

Какова пропускная способность канала?

Число знаков первичного алфавита N = 3. Из (2.17)

I₁ = - 0,2∙log₂0,2 - 0,7∙log₂0,7 - 0,1log₂0,1 = 1,16 бит,

К⁽²⁾ ≥ log₂ N = 2. Следовательно, из (5.3) и (5.4) получаем:

Скорость передачи информации.

Пусть по каналу связи за время t передано количество информации I. Можно ввести величину, характеризующую быстроту передачи информации - скорость передачи информации J:

Размерностью J, как и С, является бит/с. Каково соотношение этих характеристик? Поскольку τ₀ - минимальная длительность элементарного сигнала, очевидно, С соответствует максимальной скорости передачи информации по данной линии связи, т.е. J ≤ С или С = J_max. Таким образом,

максимальная скорость передачи информации по каналу связи равна его пропускной способности.