4.2.4. Перевод чисел между системами счисления 2 ↔ 8 ↔ 16

Интерес к двоичной системе счисления вызван тем, что именно эта система используется для представления чисел в компьютере. Однако двоичная запись оказывается громоздкой, поскольку содержит много цифр, и, кроме того, она плохо воспринимается и запоминается человеком из-за зрительной однородности (все число состоит из нулей и единиц). Поэтому в нумерации ячеек памяти компьютера, записи кодов команд, нумерации регистров и устройств и пр. используются системы счисления с основаниями 8 и 16; выбор именно этих систем счисления обусловлен тем, что переход от них к двоичной системе и обратно осуществляется, как будет показано ниже, весьма простым образом.

Двоичная система счисления имеет основанием 2 и, соответственно, 2 цифры: 0 и 1.

Восьмеричная система счисления имеет основание 8 и цифры 0, 1.....7.

Шестнадцатеричная система счисления имеет основание 16 и цифры 0, 1, ..., 9, А, В, С, D, Е, F. При этом знак «А» является 16-ричной цифрой, соответствующей числу 10 в десятичной системе; В₁₆ = 11₁₀; С₁₆ = 12₁₀; D₁₆ = 13₁₀; Е₁₆ = 14₁₀; F₁₆ = 15₁₀. Другими словами, в данном случае А ... F - это не буквы латинского алфавита, а цифры 16-ричной системы счисления и поэтому они имеют только такое начертание (не могут быть представлены в виде, например, соответствующих строчных букв, как в текстах).

Пользуясь алгоритмами, сформулированными в разделе 4.2.1, можно заполнить табл. 4.1.

Докажем две теоремы.

Теорема 1. Для преобразования целого числа Z_p → Z_q в том случае, если системы счисления связаны соотношением q = р^r, где r - целое число большее 1, достаточно Z_p разбить справа налево на группы по г цифр и каждую из них независимо перевести в систему q.

Доказательство:

Пусть максимальный показатель степени в записи числа р по форме (4.1) равен k - 1, причем, 2r > k -1 > r.

Таблица 4.1.

Вынесем множитель р^r из всех слагаемых, у которых j ≥ r. Получим:

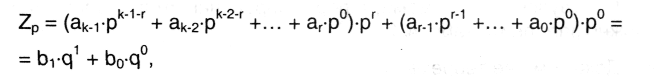
где

Таким образом, r-разрядные числа системы с основанием р оказываются записанными как цифры системы с основанием q. Этот результат можно обобщить на ситуацию произвольного k-1 > r - в этом случае выделится не две, а больше (т) цифр числа с основанием q. Очевидно, Z_q = (b_m … b₀ )_q.

Пример 4.6

Выполнить преобразование Z₂ = 110001₂ → Z₈. Исходное число разбивается на группы по три разряда справа налево (8 = 2³, следовательно, r = 3) и каждая тройка в соответствии с таблицей 4.1. переводится в 8-ричную систему счисления независимо от остальных троек:

Следовательно, 110001₂ = 61₈. Аналогично, разбивая Z₂ на группы по 4 двоичные цифры и дополняя старшую группу незначащими нулями слева, получим 110001₂= 31₁₆.

Теорема 2. Для преобразования целого числа Z_p → Z_q в том случае, если системы счисления связаны соотношением р = q^r, где r - целое число большее 1, достаточно каждую цифру Z_p заменить соответствующим r-разрядным числом в системе счисления q, дополняя его при необходимости незначащими нулями слева до группы в r цифр.

Доказательство:

Пусть исходное число содержит две цифры, т.е.

Для каждой цифры справедливо: 0 ≤ a_i ≤ р - 1 и поскольку р = q_r, 0 ≤ a_i ≤ q^r-1, то в представлении этих цифр в системе счисления q максимальная степень многочленов (4.1) будет не более r - 1 и эти многочлены будут содержать по r цифр:

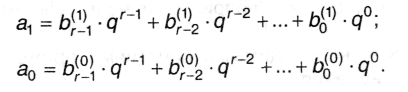
Тогда

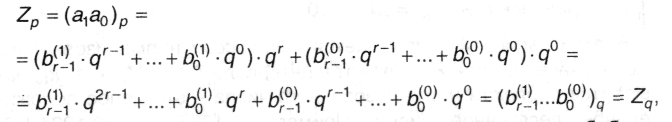
причем, число Z_q содержит 2r цифр. Доказательство легко обобщается на случай произвольного количества цифр в числе Z_p.

Пример 4.7 Выполнить преобразование D3₁₆ → Z₂.

Переходы Z₈ → Z₁₆ и Z₁₆ → Z₈, очевидно, удобнее осуществлять через промежуточный переход к двоичной системе. Например, 123₈ = 001010011₂ = 53₁₆.