4.2.3. Понятие экономичности системы счисления
Число в системе счисления р с k разрядами, очевидно, будет иметь наибольшее значение в том случае, если все цифры числа окажутся максимальными, т.е. равными р - 1. Тогда
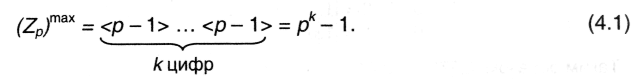
Количество разрядов числа при переходе от одной системы счисления к другой в общем случае меняется. Очевидно, если р = qσ (σ - не обязательно целое), то (Zp)max = pk - 1 = qσk - 1. Т.е. количество разрядов числа в системах счисления р и q будут различаться в σ раз. Очевидно соотношение:
При этом основание логарифма никакого значения не имеет, поскольку σ определяется отношением логарифмов. Сравним количество цифр в числе 9910 и его представлении в двоичной системе счисления: 9910 = 11000112; т.е. двоичная запись требует 7 цифр вместо 2 в десятичной, σ = ln(10)/ln(2) = 3,322; следовательно, количество цифр в десятичном представлении нужно умножить на 3,322 и округлить в большую сторону: 2-3,322 = 6,644 = 7.
Введем понятие экономичности представления числа в данной системе счисления.
Под экономичностью системы счисления будем понимать то количество чисел, которое можно записать в данной системе с помощью определенного количества цифр.
Речь в данном случае идет не о количестве разрядов, а об общем количестве сочетаний цифр, которые интерпретируются как различные числа. Поясним на примере: пусть в распоряжении имеется 12 цифр. Можно разбить их на 6 групп по 2 цифры («0» и «1») и получить шестиразрядное двоичное число; общее количество таких чисел, как уже неоднократно обсуждалось, равно 26. Можно разбить заданное количество цифр на 4 группы по три цифры и воспользоваться троичной системой счисления - в этом случае общее количество различных их сочетаний составит 34. Аналогично можно произвести другие разбиения; при этом число групп определит разрядность числа, а количество цифр в группе - основание системы счисления. Результаты различных разбиений можно проиллюстрировать таблицей:
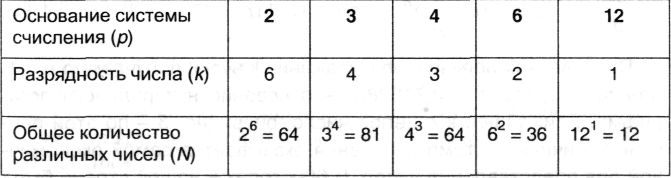
Из приведенных оценок видно, что наиболее экономичной оказывается троичная система счисления, причем, результат будет тем же, если исследовать случаи с другим исходным количеством сочетаний цифр.
Точное расположение максимума экономичности может быть установлено путем следующих рассуждений. Пусть имеется п знаков для записи чисел, а основание системы счисления р. Тогда количество разрядов числа k = п/р, а общее количество чисел (N), которые могут быть составлены, равно:
Если считать N(p) непрерывной функцией, то можно найти то значение рт, при котором iN принимает максимальное значение. Функция имеет вид, представленный на рис.4.3.
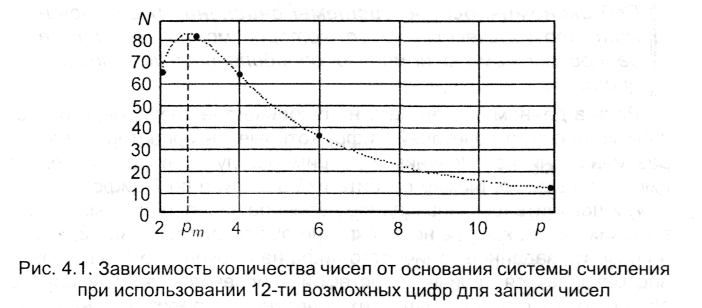
Для нахождения положения максимума нужно найти производную функции N(p), приравнять ее к нулю и решить полученное уравнение относительно р.
Приравнивая полученное выражение к нулю, получаем ln p = 1, или рт = е, где е = 2,71828... - основание натурального логарифма. Ближайшее к е целое число, очевидно, 3 - по этой причине троичная система счисления оказывается самой экономичной для представления чисел. В 60-х годах в нашей стране была построена вычислительная машина «Сетунь», которая работала в троичной системе счисления. Предпочтение все же отдается двоичной системе, поскольку по экономичности она оказывается второй за троичной, а технически она реализуется гораздо проще остальных. Таким образом, простота технических решений оказывается не единственным аргументом в пользу применения двоичной системы в компьютерах.