4.2.2. Перевод дробных чисел из одной системы счисления в другую

Вещественное число, в общем случае содержащее целую и дробную часть, всегда можно представить в виде суммы целого числа и правильной дроби. Поскольку в предыдущем параграфе проблема записи натуральных чисел в различных системах счисления уже была решена, можно ограничить рассмотрение только алгоритмами перевода правильных дробей. Введем следующие обозначения: правильную дробь в исходной системе счисления р будем записывать в виде 0, Y_р, дробь в системе q - 0, Y_q, а преобразование - в виде 0, Yp → 0, Y_q. Последовательность рассуждений весьма напоминает проведенную ранее для натуральных чисел. В частности, это касается рекомендации осуществлять преобразование через промежуточный переход к 10-ной системе, чтобы избежать необходимости производить вычисления в «непривычных» системах счисления, т.е. 0, Y_p → 0,Y₁₀ → 0,Y_q. Это, в свою очередь, разбивает задачу на две составляющие: преобразование 0, Y_р → 0, Y₁₀ и 0, Y₁₀ → 0, Y_q, каждое из которых может рассматриваться независимо.

Алгоритмы перевода 0,Y₁₀ → 0,Y_q выводится путем следующих рассуждений. Если основание системы счисления q, простая дробь содержит n цифр и b_k - цифры дроби (1 ≤ k ≤ п, 0 ≤ b_k ≤ q -1), то она может быть представлена в виде суммы:

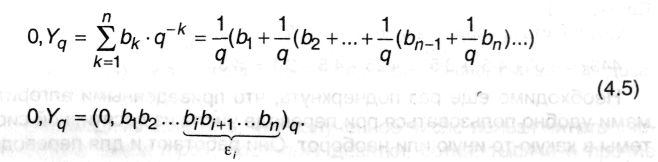
Часть дроби от разряда i до ее конца обозначим ε_i и примем ε_n = b_n/q (очевидно, ε₁ = О, Y_q); тогда в (4.5) легко усматривается рекуррентное соотношение:

Если вновь позаимствовать в PASCAL'e обозначение функции - на этот раз trunc, производящая округление целого вещественного числа путем отбрасывания его дробной части, то следствием (4.6) будут соотношения, позволяющие находить цифры новой дроби:

Соотношения (4.7) задают алгоритм преобразования 0, Y₁₀ → 0, Y_q:

1. умножить исходную дробь в 10-ной системе счисления на q, выделить целую часть - она будет первой цифрой новой дроби; отбросить целую часть;

2. для оставшейся дробной части операцию умножения с выделением целой и дробных частей повторять, пока в дробной части не окажется 0 или не будет достигнута желаемая точность конечного числа (exact); появляющиеся при этом целые будут цифрами новой дроби;

3. записать дробь в виде последовательности цифр после ноля с разделителем в порядке их появления в п. (1) и (2).

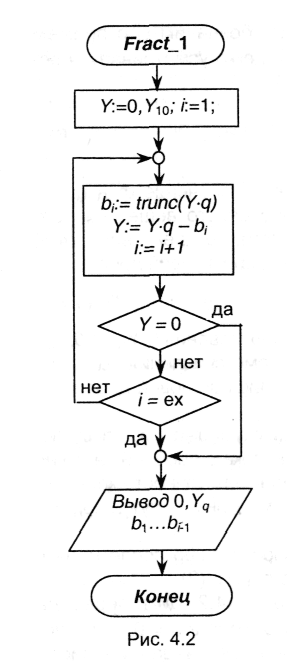
Блок-схема алгоритма представлена на рис.4.2. Цикл перевода заканчивается либо в том случае, когда окажется ε_i+1 = 0, либо последовательность действий повторится наперед заданное число раз (значение константы ех), которое совпадает с количеством значащих цифр в дробной части.

Пример 4.4.

Выполнить преобразование 0,375₁₀ → 0,Y₂

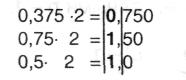
Таким образом, 0,375₁₀ = 0,011₂.

Перевод 0,Y_p → 0,Y₁₀, как и в случае натуральных чисел, сводится к вычислению значения формы (4.5) в десятичной системе счисления. Например,

Следует сознавать, что после перевода дроби, которая была конечной в исходной системе счисления, она может оказаться бесконечной в новой системе. Соответственно, рациональное число в исходной системе может после перехода превратиться в иррациональное. Справедливо и обратное утверждение: число иррациональное в исходной системе счисления в иной системе может оказаться рациональным.

Пример 4.5

Выполнить преобразование 5,3(3)₁₀ → Х₃. Перевод целой части, очевидно, дает: 5₁₀ = 12₃. Перевод дробной части: 0,3(3)₁₀ = 0,1₃. Окончательно: 5,3(3)₁₀ = 12,1₃.

Как уже было сказано, значение целого числа не зависит от формы его представления и выражает количество входящих в него единиц. Простая дробь имеет смысл доли единицы, и это «дольное» содержание также не зависит от выбора способа представления. Другими словами, треть пирога остается третью в любой системе счисления.