3.2. Способы построения двоичных кодов
3.2.1. Алфавитное неравномерное двоичное кодирование сигналами равной длительности. Префиксные коды
Как следует из названия, в способах кодировании, относящихся к этой группе, знаки первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Длительности элементарных сигналов при этом одинаковы (τ0 = τ1 = τ). Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время K(A,2) ∙ τ. Таким образом, задачу оптимизации неравномерного кодирования можно сформулировать следующим образом: построить такую схему кодирования, в которой суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей. За счет чего возможна такая оптимизация? Очевидно, суммарная длительность сообщения будет меньше, если применить следующий подход: тем знакам первичного алфавита, которые встречаются в сообщении чаще, присвоить меньшие по длине коды, а тем, относительная частота которых меньше - коды более длинные. Другими словами, коды знаков первичного алфавита, вероятность появления которых в сообщении выше, следует строить из возможно меньшего числа элементарных сигналов, а длинные коды использовать для знаков с малыми вероятностями.
Параллельно должна решаться проблема различимости кодов. Представим, что на выходе кодера получена следующая последовательность элементарных сигналов:
00100010000111010101110000110
Каким образом она может быть декодирована? Если бы код был равномерным, приемное устройство просто отсчитывало бы заданное (фиксированное) число элементарных сигналов (например, 5, как в коде Бодо) и интерпретировало их в соответствии с кодовой таблицей. При использовании неравномерного кодирования возможны два подхода к обеспечению различимости кодов.
Первый состоит в использовании специальной комбинации элементарных сигналов, которая интерпретируется декодером как разделитель знаков. Второй - в применении префиксных кодов. Рассмотрим подробнее каждый из подходов.
Неравномерный код с разделителем
Условимся, что разделителем отдельных кодов букв будет последовательность 00 (признак конца знака), а разделителем слов-слов - 000 (признак конца слова - пробел). Довольно очевидными оказываются следующие правила построения кодов:
код признака конца знака может быть включен в код буквы, поскольку не существует отдельно (т.е. кода всех букв будут заканчиваться 00);
коды букв не должны содержать двух и более нулей подряд в середине (иначе они будут восприниматься как конец знака);
код буквы (кроме пробела) всегда должен начинаться с 1;
разделителю слов (000) всегда предшествует признак конца знака; при этом реализуется последовательность 00000 (т.е., если в конце кода встречается комбинация ...000 или ...0000, они не воспринимаются как разделитель слов); следовательно, коды букв могут оканчиваться на 0 или 00 (до признака конца знака).
В соответствии с перечисленными правилами построим кодовую табл. 3.1 для букв русского алфавита, основываясь на приведенных ранее (табл. 2.1.) вероятностях появления отдельных букв.
Теперь по формуле (А.11) можно найти среднюю длину кода К(r,2) для данного способа кодирования:
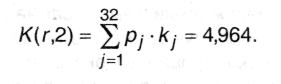
Поскольку для русского языка, как указывалось в п.2.3., I1(r) = 4,356 бит, избыточность данного кода, согласно (3.5), составляет:
это означает, что при данном способе кодирования будет передаваться приблизительно на 14% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение К(е,2) = 4,716, что при I1(e) = 4,036 бит приводят к избыточности кода Q(е,2) = 0,168.
Таблица 3.1.
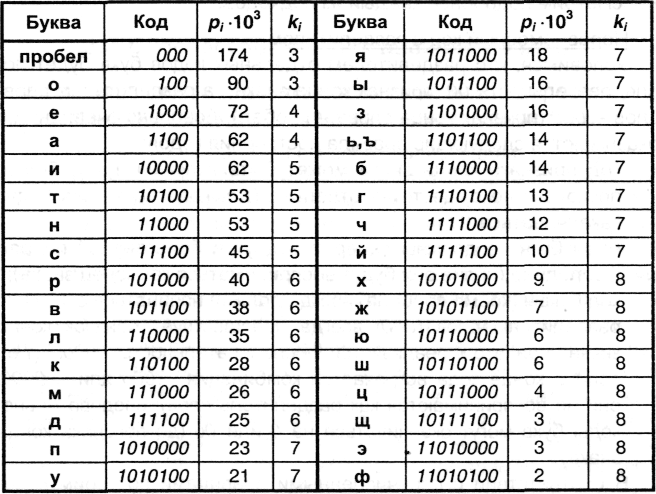
Рассмотрев один из вариантов двоичного неравномерного кодирования, попробуем найти ответы на следующие вопросы: возможно ли такое кодирование без использования разделителя знаков? Существует ли наиболее эффективный (оптимальный) способ неравномерного двоичного кодирования?
Суть первой проблемы состоит в нахождении такого варианта кодирования сообщения, при котором последующее выделение из него каждого отдельного знака (т.е. декодирование) оказывается однозначным без специальных указателей разделения знаков. Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию Фано):
Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом*) какого-либо иного более длинного кода.
* В языковедении термин «префикс» означает «приставка».
Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления с таблицей кодов всегда можно точно указать, где заканчивается один код и начинается другой.
Пример 3.1.
Пусть имеется следующая таблица префиксных кодов:
Требуется декодировать сообщение:
00100010000111010101110000110
Декодирование производится циклическим повторением следующих действий:
(a) отрезать от текущего сообщения крайний левый символ, присоединить справа к рабочему кодовому слову;
(b) сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (а);
(c) декодировать рабочее кодовое слово, очистить его;
(d) проверить, имеются ли еще знаки в сообщении; если «да», перейти к (а).
Применение данного алгоритма дает:
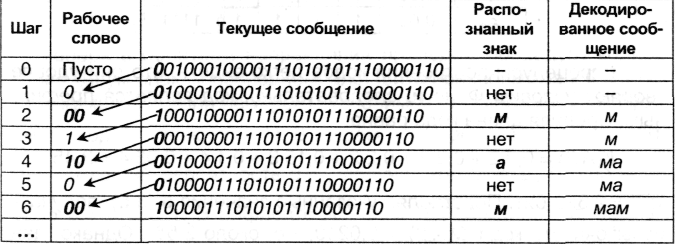
Доведя процедуру до конца, получим сообщение: «мама мыла раму».
Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных. Мы рассмотрим две схемы построения префиксных кодов.
Префиксный код Шеннона-Фано
Данный вариант кодирования был предложен в 1948-1949 гг. независимо Р. Фано и К. Шенноном и по этой причине назван по их именам. Рассмотрим схему на следующем примере: пусть имеется первичный алфавит А, состоящий из шести знаков а1 ...а6 с вероятностями появления в сообщении, соответственно, 0,3; 0,2; 0,2; 0,15; 0,1; 0,05. Расположим эти знаки в таблице в порядке убывания вероятностей (см. табл. 3.2). Разделим знаки на две группы таким образом, чтобы суммы вероятностей в каждой из них были бы приблизительно равными. В нашем примере в первую группу попадут a1 и а2 с суммой вероятностей 0,5 - им присвоим первый знак кода "0". Сумма вероятностей для остальных четырех знаков также 0,5; у них первый знак кода будет "1". Продолжим деление каждой из групп на подгруппы по этой же схеме, т.е. так, чтобы суммы вероятностей на каждом шаге в соседних подгруппах были бы возможно более близкими. В результате получаем:
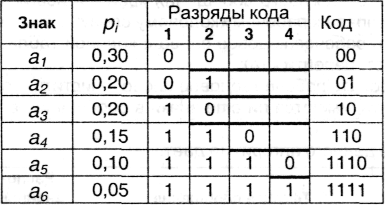
Из процедуры построения кодов легко видеть, что они удовлетворяют условию Фано и, следовательно, код является префиксным. Средняя длина кода равна:
I1(A) = 2,390 бит. Подставляя указанные значения в (3.5), получаем избыточность кода Q(A,2) = 0,0249, т.е. около 2,5%. Однако, данный код нельзя считать оптимальным, поскольку вероятности появления 0 и 1 неодинаковы (0,35 и 0,65, соответственно). Применение изложенной схемы построения к русскому алфавиту дает избыточность кода 0,0147.
Префиксный код Хаффмана
Способ оптимального префиксного двоичного кодирования был предложен Д. Хаффманом. Построение кодов Хаффмана мы рассмотрим на том же примере. Создадим новый вспомогательный алфавит A1, объединив два знака с наименьшими вероятностями (а5 и а6) и заменив их одним знаком (например, а(1)); вероятность нового знака будет равна сумме вероятностей тех, что в него вошли, т.е. 0,15; остальные знаки исходного алфавита включим в новый без изменений; общее число знаков в новом алфавите, очевидно, будет на 1 меньше, чем в исходном. Аналогичным образом продолжим создавать новые алфавиты, пока в последнем не останется два знака; ясно, что количество таких шагов будет равно N - 2, где N - число знаков исходного алфавита (в нашем случае N = 6, следовательно, необходимо построить 4 вспомогательных алфавита). В промежуточных алфавитах каждый раз будем переупорядочивать знаки по убыванию вероятностей. Всю процедуру построения представим в виде таблицы:
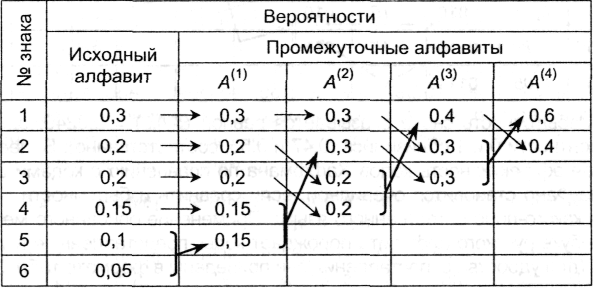
Теперь в обратном направлении проведем процедуру кодирования. Двум знакам последнего алфавита присвоим коды 0 и 1 (которому какой - роли не играет; условимся, что верхний знак будет иметь код 0, а нижний - 1). В нашем примере знак а1(4) алфавита A(4), имеющий вероятность 0,6, получит код 0, а a2(4) с вероятностью 0,4 - код 1. В алфавите А(3) знак a1(3) получает от a2(4) его вероятность 0,4 и код (1); коды знаков a2(3) и a3(3), происходящие от знака a1(4) с вероятностью 0,6, будут уже двузначным: их первой цифрой станет код их «родителя» (т.е. 0), а вторая цифра - как условились - у верхнего 0, у нижнего - 1; таким образом, a2(3) будет иметь код 00, а a3(3) - код 01. Полностью процедура кодирования представлена в таблице, приведенной на с.70.
Из процедуры построения кодов вновь видно, что они удовлетворяют условию Фано и, следовательно, не требуют разделителя. Средняя длина кода, как и в предыдущем примере оказывается:
К(А,2) = 0,3 ∙ 2 + 0,2 ∙ 2 + 0,2 ∙ 2 +0,15 ∙ 3 + 0,1 ∙ 4 + 0,05 ∙ 4 = 2,45.
Избыточность снова оказывается равной Q(A, 2) = 0,0249, однако, вероятности 0 и 1 сблизились (0,47 и 0,53, соответственно). Более высокая эффективность кодов Хаффмана по сравнению с кодами Шеннона-Фано становится очевидной, если сравнить избыточности кодов для какого-либо естественного языка. Применение описанного метода для букв русского алфавита порождает коды, представленные в табл. 3.2. (для удобства сопоставления они приведены в формате табл. 3.1).
Таблица 3.2
Средняя длина кода оказывается равной К(r,2) = 4,395; избыточность кода Q(r,2) = 0,0090, т.е. не превышает 1 %, что заметно меньше избыточности кода Шеннона-Фано (см. выше).
Код Хаффмана важен в теоретическом отношении, поскольку можно доказать, что он является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана (см. [49, с.209-211]).
Таким образом, можно заключить, что существует способ построения оптимального неравномерного алфавитного кода. Не следует думать, что он представляет число теоретический интерес. Метод Хаффмана и его модификация - метод адаптивного кодирования (динамическое кодирование Хаффмана) - нашли широчайшее применение в программах-архиваторах, программах резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах.