
- •1.Комплексные числа и действия над ними
- •2. Свойства модуля и аргумента
- •3. Последовательность комплексных чисел.
- •4. Бесконечность и стереографическая проекция.
- •5. Множества точек на плоскости.
- •6. Понятие фкп. Предел и непрерывность фкп.
- •7. Дифференцируемость фкп.
- •8. Необходимые и достаточные условия дифференцируемости (доказать необходимость)
- •9. Необходимые и достаточные условия дифференцируемости (доказать достаточность).
- •10. Гармонические функции.
- •11. Геометрический смысл аргумента производной.
- •12. Геометрический смысл модуля производной.
- •13. Понятиео конформных отображениях.
- •14. Линейная функция.
- •15. Отображение .
- •16. Дробно-линейная функция.
- •17. Конформность дробно-линейной функции.
- •18. Параметры и инвариант дробно-линейного отображения.
- •19. Отображения областей, ограниченных прямыми или
- •20. Круговое свойство дробно-линейной функции.
- •21. Свойство симметрии дробно-линейной функции.
- •26. Показательная функция.
- •27. Логарифмическая функция.
- •28. Общая степенная функция.
- •29. Функция Жуковского.
- •30. Тригонометрическая функция.
- •31. Одназначные ветви многозначной функций .
- •32. Поверхность Римана .
- •33. Однозначные ветви многозначной функции и ее поверхность Римана.
- •34. Интеграл от фкп и его свойства.
- •35. Сведение вычисления интеграла от фкп к вычислению обыкновенного интеграла.
- •36. Интегральная теорема Коши для простого контура.
- •37. Интегральная теорема Коши для составного контура.
- •38. Неопределенный интеграл в комплексной области.
- •39. Интегральная формула Коши.
- •40. Интеграл типа Коши.
- •41. Бесконечная дифференцируемость аналитической функции.
- •42. Обращение интегральной теоремы.
- •43. Числовые ряды.
- •44. Функциональные ряды.
- •45.Степенные ряды. Теорема Абеля.
- •46.Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать первую часть).
- •47. Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать вторую часть).
- •48. Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать третью часть).
- •49. Приложение теоремы Вейерштрасса к степенным рядам.
- •50. Теорема Тейлора.
- •51. Неравенство Коши для коэффициентов степенного ряда.
- •52. Теорема Лиувилля.
- •53. Свойства единственности аналитических функций.
- •54. Свойство единственности аналитических функций (доказать вторую часть)
- •55. Нули аналитических функций
- •56. Принцип максимума модуля.
- •57. Ряд Лорана и его область сходимости
- •58. Теорема Лорана
- •59. Классификация изолированных особ. Точек однознач. Аналитической ф-ции.
- •60. Устранимая особая точка.
- •61. Полюс.
- •62. Связь между нулем и полюсом.
- •63. Разложение аналитич. Ф-ции в ряд Лорана в окрес-ти бесконечно удаленной точки (б.У.Т.).
- •64. Теорема Сохоцкого-Вейерштрасса.
- •65. Вычет. Основная теорема о вычетах.
- •66. Вычисление вычетов относительно простого полюса.
- •67. Вычисление вычетов относительно кратного полюса.
- •68. Вычет относительно бесконечно удаленной точки.
- •69. Вычисление интегралов вида .
- •70. Вычисление интегралов вида .
- •71. Лемма Жордана.
- •72. Логарифмический вычет
- •73. Принцип аргумента
- •74. Теорема Руше
- •75. Теорема Гурвица
- •76. Целые функции
- •77. Разложение целой функции в произведение.
- •78. Мероморфные функций.
- •79. Разложение Миттаг-Леффлера.
33. Однозначные ветви многозначной функции и ее поверхность Римана.
Рассмотри
функцию
.
Функция
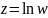 является обратная по отношению к функций
,
как известно функция
является многозначной, а именно
бесконечнозначной.
является обратная по отношению к функций
,
как известно функция
является многозначной, а именно
бесконечнозначной.
Найдем
область одноместности для функций
. Пусть
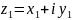 и
и
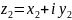 тогда равенство
тогда равенство
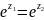 т.к
т.к
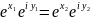
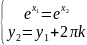 <=>
<=>
Поэтому за область можно взять любую горизонтальную полосу шириной .
Как
известно функция
прямую
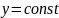 переводит в луч плоскости
.
Отсюда следует, что полоса
переводит в луч плоскости
.
Отсюда следует, что полоса
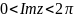 плоскости
перейдет в плоскость
с выбрашеной положительной, частью
полюса. Эти функций рассмотрим как
различных ветвей многозначн функция
плоскости
перейдет в плоскость
с выбрашеной положительной, частью
полюса. Эти функций рассмотрим как
различных ветвей многозначн функция
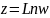 .
Функция
имеет очевидно
множество
ветвей, чтобы фиксировать какую-либо
из этих ветвей достаточно лишь указать
в какой из областей изменится
.
.
Функция
имеет очевидно
множество
ветвей, чтобы фиксировать какую-либо
из этих ветвей достаточно лишь указать
в какой из областей изменится
.
Фиксируя
какую-нибудь из ветвей
, к-фиксированая, заставим точку
описать
замкнутую кривую и получим, что точка
и
являются точками разветления функций
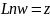 .
.
Совершая обороты мы никогда не вернемся к исходному значению. Точка наз разветвлением порядка или трансцендентной точкой ветвления.
34. Интеграл от фкп и его свойства.
П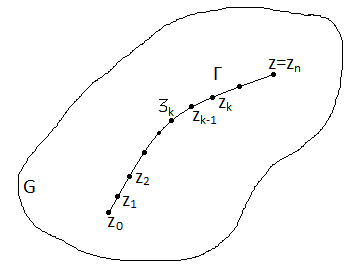 усть
в области
плоскость
усть
в области
плоскость
 определена непрерывной функцией
.
Пусть
-произвольная
гладкая линия, лежащая в этой области
с началом в точке
и
концом в точке
.
определена непрерывной функцией
.
Пусть
-произвольная
гладкая линия, лежащая в этой области
с началом в точке
и
концом в точке
.
Линия называется гладкой, если для неё можно указать параметрическое представление:
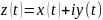 ,
,
такое
что функции
 имеют
непрерывную производную 1-го порядка,
которая не обращается одновременно в
0 на
имеют
непрерывную производную 1-го порядка,
которая не обращается одновременно в
0 на
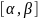 .
.
Разобьём
линию
на произвольное число
частичных дуг с помощью точек
 расположенных в положительном направлении
линии
.
расположенных в положительном направлении
линии
.
Обозначим
через
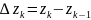 ,
,
 -произвольную
точку, расположенную на частичной дуге
с началом в точке
-произвольную
точку, расположенную на частичной дуге
с началом в точке
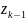 и концом в точке
и концом в точке
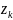 .
.
 (1)
- интегральная сумма.
(1)
- интегральная сумма.
Пусть
 .
Заставим
.
Заставим
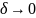 .
.
Докажем, что интегральная сумма (1) будет стремится к определённому конечному пределу независящему ни от способа разбиения кривой на частичные дуги, ни от выбора на них точек .
Введем
обозначения:
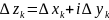 ;
;
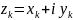 ;
;
 ;
;
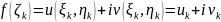 .
.
Тогда
сумма (1) примет вид:
 (2)
(2)
Так как функция непрерывна, то непрерывными будут и функции и .
Очевидно,
что если
,
то
 .
.
На
основании известной теоремы из
математического анализа обе суммы
правой части равенства (2) стремятся
соответственно к пределам:
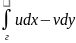 и
и
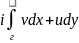 .
.
Следовательно, левая часть равенства (2) также стремится к определённому пределу, когда .
Этот
предел называется интегралом от
функции
вдоль
линии
и обозначается:
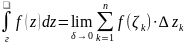 .
.
И
так имеем:
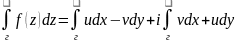 (3)
(3)
Линия называется путём или контуром интегрирования.
Формула (3) даёт выражения интеграла по комплексному переменному, через 2 действительных КрИ-2.
Формулу
(3) легко запомнить, если записать её
формально в следующем виде:
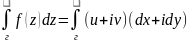 .
.
Свойства:
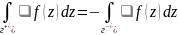 ,
где
,
где
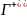 и
и
 обозначают один и тот же путь интегрирования
проходимый соответственно в положительном
и отрицательном направлении.
обозначают один и тот же путь интегрирования
проходимый соответственно в положительном
и отрицательном направлении. ,
где
,
где
 .
.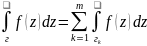 ,
где
,
где .
Все эти свойства выполняются как
следствия из известных свойств КрИ-2.
.
Все эти свойства выполняются как
следствия из известных свойств КрИ-2. ,
здесь в правой части фигурирует КрИ-1,
т.е. интеграл по длине дуги.
,
здесь в правой части фигурирует КрИ-1,
т.е. интеграл по длине дуги.если
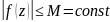 для
для
 ,
,
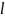 -
длина
,
то из 4) легко получить более простое,
но менее точную оценку:
-
длина
,
то из 4) легко получить более простое,
но менее точную оценку:
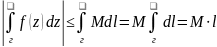 .
.
