26. Показательная функция.

Функция определяющая соотношением называется показательная функция.

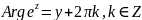
Свойства.

1.

2.Показательная функция не обратима в нуль нигде на плоскости для

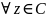
Док-во. при

3.

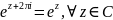
4.Функция является аналитической во всей комплексной плоскости .

27. Логарифмическая функция.

Опр.Логарифмические комплексные числа называется такое комплексное число , что и обозначается .

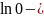не сущ, т.к . Пусть

Получим:

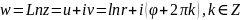, т.е

или

Значение функций соответственно некоторому фиксированному значению наз ветвью.

Ветвью соответственно наз главная и обозначается

28. Общая степенная функция.

Под степенной функцией с производной показательной понимают . Обозначаются какое-нибудь из значений , тогда все значения можно получить: Согласно,

1. пусть целое число , тогда . Т.к целое число, поэтому одназначно.

2. дробно рациональное число, несократимая дробь.

- это выражение может принимать лишь различных значений соответственно

3. иррациональных число или чисто мнимое, то бесконечнозначно.

Док-во. Если преложить, что среди них есть равные, то

или

- рациональное число!!!

29. Функция Жуковского.

Рассмотри функцию . Эта функция называется функцией Жуковского.

Т.к. , то её множество значений принимаемые во внутренней и во внешности, единичного круга, одинаковы.

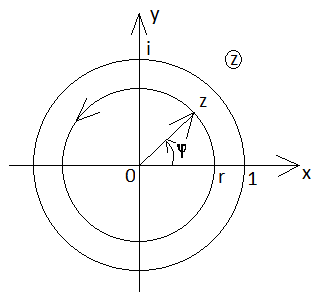
Исследуем отображение осуществляемое функцией Жуковского. Для этого найдем образы окружности и радиусов . При этом мы можем ограничится, например, только внутренностью единичного круга.

Положим: , т.е. , , .

Тогда или , , . (1)

Отсюда исключая параметр получаем:

(2)

Это и есть уравнение эллипса с полуосями , и фокусами , т.к. .

30. Тригонометрическая функция.

Осн тригонометрические функций и определены.

,

чётная, а нечетная,т.к

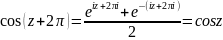
4=1

31. Одназначные ветви многозначной функций .

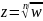Пусть , тогда получаем различных значений многозначной функций соответственно различными ветвями. Выберем , т.е фиксир. Заставим точку плоско описать некоторую замкнутую кривую . Пусть эта кривая не заключает в себя начало координат. Тогда изменяющая и вернутся опять к первоначальному значению, когда примет исходное положение. Предположим, что т опишет замк кривую , содерж внутри себя начало координат увеличваеться на .

Значит

Тогда обладающая тем свойством, что обход вокруг нее переводит нас от данной ветви к другой наз точкой разветления данной функций, тогда, точка является точкой развлетления для , при этом говорят, что точка равная для является мог разветления конечного порядка или алгебраической точкой разветления.

32. Поверхность Римана .

Будем считать, что производная разрезанной плоскости по положительной части оси . Установим взаимноодназных соответствий между верхнем берегом разреза и лучем , между нижним и также отображение взаимно одназначно на плоскости с разрезом по + дейст оси и.т.д. У нас есть экземпляров. Сектору плоскости ставят й лист плоскости . Луч переходит в верх берег разреза к-го листа. Чтобы была непрерывная, нужно склеить нижний берег разреза к-го листа с верхним берегом разреза к+1-го листа при этом свободен верхний берег разреза 1-го листа и нижний берег го листа.

Функция полной плоскости ставят в соответствие листов плоскости , склеенных указанным способом.

Такое геом многообразие представляет собой частные случай так называются поверхности Римана.

Функция наз листной. принадлежит всем листам поверхности Римана и наз точной разветления для функций .