19. Отображения областей, ограниченных прямыми или

окружностями.

Теорема: Каковы бы ни были прямые или окружности и и две тройки чисел и принадлежащих соответственно и , существует дробно-линейная функция отображающая так, что точки .

Доказательство: Построим дробно-линейную функцию удовлетворяющую условиям: , ;

Такая функция существует и оно единственна.

В силу кругового свойства, эта функция прямую или окружность отображает на прямую или окружность .

Но проходит через точки поэтому проходит через точки , а так как через 3 точки нельзя провести двух различных прямых или окружностей, то совпадает с .

Пусть теперь некоторая дробно-линейная функция отображает окружность в окружность , так, что 3 точки .

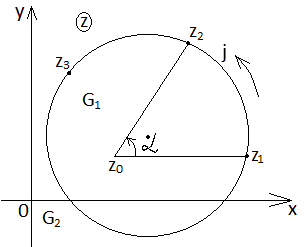
Рассмотрим следующую задачу, что будет являться образом областе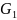й и , покажем, что:

1. если направление обхода точек и точек совпадаю, то , ;

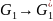2. если направление обхода точек и точек различно, то , ;

Действительно пусть направление обхода точек совпадаю, возьмём произвольную точку и предположим, что её образам является точка . Соединим точку отрезками прямых и . Обозначим угол между ними . В силу кругового свойства эти отрезки перейдут в прямые или дуги окружностей проходящие через точки .

По свойству конформности дробно-линейной функции, угол между и должен быть равен как по величине, так и по направлении отсчёта, однако, если точка лежит в 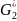, то направление отсчёта будет иным, чем в плоскости . Это противоречие и доказывает, что , а это означает, что .

Остальные случаи рассматриваются аналогично.

Приведенное утверждение сохраняет силу и в случае, когда одну или обе окружности заменить прямыми.

20. Круговое свойство дробно-линейной функции.

Теорема: Образом прямой или окружности при любом дробно-линейном преобразовании является прямая или окружность.

Замечание: Если заданная прямая или окружность, то легко установить, перейдёт она при дробно-линейном преобразовании в прямую или окружность.

Действительно, в результате отображения мы получим прямую только в том случае, когда на заданной прямой или окружности лежит точка, которая дробно-линейным отображением переводится в бесконечно удалённую точку.

Можно отметить, что считая прямую линию за окружность бесконечно большого радиуса круговое свойство можно сформулировать так: при дробно-линейном преобразовании окружность переходит в окружность.

21. Свойство симметрии дробно-линейной функции.

Две точки наз симметричными относительно окружности , если она лежит на одной полупрямой, выходящей из центра так, что произведения их расстояний от центра окружности равно . Если точка есть центр окружности, то ей симметричной полагают точку бесконечность.

В случае, если является прямой, то симметричной будем наз точки, полученные друг у друга зеркальным отображением относительно данной прямой.

Лемма1: Если через точку, лежащую вне окружности провести касательную и секущую, то произведение всей секущей на её внешнюю часть равно квадрату касательной.

Док-во.

Рассмотрим треугольники Они подобные, т.к. все углы равны: .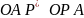

Лемма2: Если т . принадлежит окружности, а через т. , лежащую вне этой окружности проведена секущая и , то - касательная.

Лемма3: Если точки симметричны относительно окружности , то пучок окружностей, проходящих через эти точки, ортогонален .

Лемма4:Если пучок окружностей, проходящих через ортогонален окружности , то точки симметричны относительно .

Теорема: дробно-линейная функция переводит симметричные точки относительно окружности (прямой) в симметричные точки относительно ее образа.

22. Отображение верхней полуплоскости на верхнюю полуплоскость с помощью дробно-линейной функций.

Верхнюю полуплоскость можно рассматривать, как частный случай круга радиуса.

Чтобы верхняя полуплоскость перешла на верхнюю полуплоскость необх, перевести действительную ось, ограниченную верхнюю полуплоскость, саму на себя.

23. Отображение верхней полуплоскости на единичный круг, с помощью дробно-линейной функций.

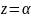Т Очевидно, что т симметрична с т . относительно действительной оси, а т симметрична с т относительно окружности .

, где

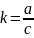
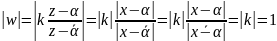
24. Отображение единично круга на единичный круг с помощью дробно-линейной функций.

Будем строить искомое отображение в виде дробно линейной функций так , точка очевидно симметрично с точкой относительно окружности .

, то . А точка симетрична точки относительно окружности

. Тогда 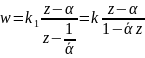, где

Окружность переходит в окружность , то

=

,

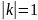
25. Степенная функция.

Под степенной функцией с производной показательной понимают . Обозначаются какое-нибудь из значений , тогда все значения можно получить: Согласно,

1. пусть целое число , тогда . Т.к целое число, поэтому 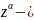одназначно.

2. дробно рациональное число, несократимая дробь.

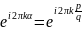- это выражение может принимать лишь различных значений соответственно

3. иррациональных число или чисто мнимое, то бесконечнозначно.

Док-во. Если преложить, что среди них есть равные, то

или

- рациональное число!!!