10. Гармонические функции.

В дальнейшем будет показано, что действительные и мнимые части и функции аналитической в некоторой области, обладает в этой области непрерывными частными производными любого конечного порядка.

Пусть функция - аналитична в области , тогда всюду в этой области выполняются условия Коши-Римана: ,

Тогда дифференцируя первое из этих условий по , а второе по , и складывая почленно оба результата, получим:

(1) – уравнение Лапласа.

Аналогичное уравнение получится и для функции , если первое уравнение продифференцировать по , а второе по .

Уравнение (1) является дифференциальным уравнением с частными производными второго порядка и называется уравнением Лапласа.

Любая функция, обладающая в некоторой области непрерывными частными производными до 2 порядка включительно, и удовлетворяющие уравнению Лапласа называется гармонической этой области.

Если гармонические функции и связаны в области уравнения Коши-Римана, то они называются сопряжёнными гармоническими функциями.

Следовательно, действительные и мнимые части функции аналитической в некоторой области являются сопряжёнными гармоническими функциями в той же области.

Теорема: По любой функции ( ) гармонической в односвязной области , можно найти такую аналитическую функцию , действительная (мнимая) часть которой совпадает с .

11. Геометрический смысл аргумента производной.

Пусть есть функция аналитическая в некоторой области . Значение функции будем изображать точками плоскости , а точки - плоскости .

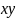Кроме того будем считать, что положения направления осей и совпадают.

При движении точки в плоско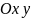сти соответствующая ей точка будет описывать плоскости 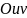некоторую линию .

Пусть – произвольная точка области и пусть – данная линия со своим направлением, выходящая из точки и имеющая определённую касательную в этой точке.

В плоскости ей будет соответствовать некоторая линия выходящая из точки .

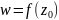Предположим, что . Выясним геометрический смысл производной . Для этого предварительно представим комплексное число в тригонометрической форме: .

Выясним геометрический смысл (аргумента) производной и её модуля .

Возьмём произвольную точку на линии и обозначим через 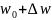соответствующую ей точку на линии .

Очевидно, при стремлении точки по линии к точке соответствующая ей точка - к по линии . Причём 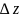и одновременно будут стремиться к нулю.

Т.к. , т.к. очевидно (1) (2)

Замечание: В равенстве (1) мы использовали, что , т.к. в противном случае угол не имел бы определённого значения.

Рассмотрим сначала равенство (1), т.к. с точностью до кратных : 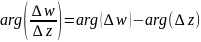, то равенство (1) примет вид: 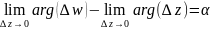(1)*

Выясним геометрический смысл равенства (1) пользуясь рисунками.

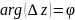, ; тогда равенство (1)* можем записать в виде:

(1)**

В пределе направление вектора совпадает с направлением касательной к линии в точке , а к линии в точке . Последняя касательная необходима, должна существовать в силу равенства (1)**. Обозначим через и углы осей и соответственно с касательной и в точках и .

Тогда: , или (3)

Будем считать положительным направления и совпадают между собой. Тогда из (3) видим, что – есть угол между первоначальным и отображённым направлением, т.е. угол поворота касательной. В этом и заключается геометрический смысл аргумента производной

Заметим далее, что линию мы берем произвольной. При изменении линии будут изменяться углы и , но будет постоянен.

И так, отображение с помощью аналитической функции обладает свойствами сохранения (консерватизма) углов во всех точках, где .