6. Понятие фкп. Предел и непрерывность фкп.

Определение: Пусть Е-некоторое мн-во точек компл пл-ти, если поставлено в соответствие одно или несколько комплексных чисел w, то говорят,что на мн-ве Е определена ф-ция .

Если каждому z соотв одно значение w, то ф-ция наз однозначной; если z соотв более одного значения, то – многозначной.

Примеры. Однозначные: определены на всей компл пл-ти. Многозначные ( -значные)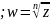 (n-значная).

Одно компл соотношение равносильно 2 действительным

Переход от записи к наз выделением действит и мнимой частей ФКП.

Опр: Компл число А наз пределом в точке , если и пишут

Определение: Если то функ наз непрерывной в точке .

Определение: Функ непрер в каждой точке некоторой обл G наз непрер в этой обл.

Непрер эквивалентна непрер 2 действит функц и .

Если непрер в точке непрер в , то сложная функ непрер в

7. Дифференцируемость фкп.

Определение: Пусть однозначная функция определена в некоторой окресности точки .Если существ , то этот конечный предел наз производной функ в точке ; сама функ наз дифференцируемой в точке .

Определение: Если дифференцируема в каждой точке обл G, то она наз аналитической в этой обл.

8. Необходимые и достаточные условия дифференцируемости (доказать необходимость)

Выше было отмечено, что непрерывность функций в т. равносильно непрерывная функция и в точке .

Как видно из рассмотренного нами примера 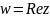такое утверждение не имеет место в случае диф. Из того, что функция и имеют частные производные ещё не следует существование производной функций . Т.о. в случае диф функций её действит часть и мнимая часть должны быть выбраны не незав другом друга, а так чтобы выполнялись некоторые дополнительные условия.

Предварительно напомним некоторые сведения из мат. анализа.

Функция 2-х действительных переменных наз диф в т , если ее приращение можно представить

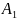в виде где, , а и 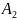не зависит от и . При этом оказывается, что они равны частичным производным функций в т. , ,

Теорема.1)Для того, чтобы функция была диф в т как функция комплексного переменного необх и достаточно, чтобы функция и были диф в той же точки как функции 2-х действительных переменных и, чтобы в этой точке выполнились условия.

,

При выполнений всех условий теоремы производная

может быть вычислена по одной из следующих формул

наз условия Коши-Римана.

Док-во.(Необходимости)

Пусть 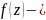диф т тогда сущ конечный предел

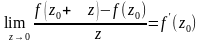положим , тогд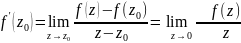а . Отсюда 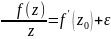или где

.

,

, ,

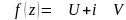
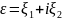Подставляя найденные выражения в соотношение (1) и отделяя действит и мнимыя части, будем иметь

Отсюда в силу того, что при вытекает

1)Функция и 2-х действит переменных и

диф в т.

2)Их частные простые в этой точки такавы

. И следовательно удовлетворяет условием Наконец Необх доказана.

9. Необходимые и достаточные условия дифференцируемости (доказать достаточность).

Теорема.1)Для того, чтобы функция была диф в т как функция комплексного переменного необх и достаточно, чтобы функция и были диф в той же точки как функции 2-х действительных переменных и, чтобы в этой точке выполнились условия.

,

При выполнений всех условий теоремы производная

может быть вычислена по одной из следующих формул

наз условия Коши-Римана.

Док-во.

Пусть функция и диф в точке и в этой точке выполнялись условия Коши-Римана.

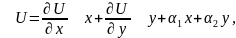
, где при . Кроме того

Следовательно

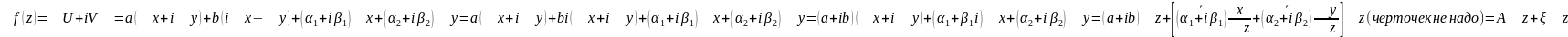
Т.к при

То отсюда и соотношение (2) следует, что диф в т и ее производная