79. Разложение Миттаг-Леффлера.
Рассмотрим
случай когда число полюсов мероморфной
функций бесконечно. Не трудно показать,
что все полюсы мероморфной функций
можно перенумировать
и расположить их в последовательность
в порядке неубывающих модулей
Пусть
обозначает главную часть разложения
Лорана мероморфной функций
в окрестности полюса
т.е
,где
-
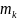порядок полюса
.
Можно
попытаться и в общем случае поступать
также как мы выше
поступили в случае мероморфной функций
с конечным числом полюсов, а именно
вычесть сумму всех главных частей из
с тем, чтобы в разности получить функцию,
не имеющих особых точек в конечной
плоскости, т.е целую функцию. Однако в
данном случае множество главных частей
бесконечно, и нет
гарантии, что ряд
сходятся.
Шведский
математик Меттал-Леффлер преодалел эту
трудность. Он показал, что всегда можно
подобрать такие многочлены
, что ряд
будет
равномерно сходится в любом круге
,
если из этого круга исключить попадающие
в него точки
полюсы членов ряда (1) .
Предполагаем, что такие члены найдены, получим, что функция
представляет
собой аналитичную
функцию,
имеющую
полюса в тех же точках
,
в которых имеет полюсы и функция
,
при этом главные части Лорановских
разложений
функций
в окрестности точек
есть
одни и теже рациональные функций
.
Поэтому
разность
есть целая функция, при этом получаем
формулу.
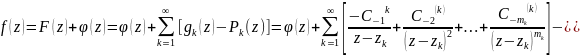
Это и есть так называемый Миттаг-Леффлеровское разложение функций . Его можно рассмотреть как разложение мероморфной функций на простейшие дроби .
Комплексные числа и их геометрическая интерпретация.
Свойства модуля и аргумента.
Последовательности комплексных чисел.
Бесконечность и стереографическая проекция.
Множества точек на плоскости.
Понятие ФКП. Предел и непрерывность ФКП.
Дифференцируемость ФКП.
Необходимые и достаточные условия дифференцируемости. (доказать необходимость).
Необходимые и достаточные условия дифференцируемости. (доказать достаточность).
Гармонические функции.
Геометрический смысл аргумента производной.
Геометрический смысл модуля производной.
Понятиео конформных отображениях.
Линейная функция.
Отображение
.Дробно-линейная функция.
Конформность дробно-линейной функции.
Параметры и инвариант дробно-линейного отображения.
Отображения областей, ограниченных прямыми или окружностями.
Круговое свойство дробно-линейной функции.
Свойство симметрии дробно-линейной функции.
Отображение верхней полуплоскости на верхнюю полуплоскость с помощью дробно-линейной функции.
Отображение верхней полуплоскости на единичный круг, с помощью дробно-линейной функции.
Отображение единичного круга на единичный круг с помощью дробно-линейной функции.
Степеннаяфункция.
Показательная функция.
Логарифмическая функция.
Общая степенная функция.
Функция Жуковского.
Тригонометрические функции.
Однозначные ветви многозначной функции .
Поверхность Римана функции .
Однозначные ветви многозначной функции и её поверхность Римана.
Интеграл от ФКП и его свойства.
Сведение вычисления интеграла от ФКП к вычислению обыкновенного интеграла.
Интегральная теорема Коши для простого контура.
Интегральная теорема Коши для составного контура.
Неопределённый интеграл в комплексной области.
Интегральная формула Коши.
Интеграл типа Коши.
Бесконечная дифференцируемость аналитической, функции.
Обращение интегральной теоремы.
Числовые ряды.
Функциональные ряды.
Степенные ряды. Теорема Абеля.
Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать первую часть).
Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать вторую часть).
Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать третью часть).
Приложение теоремы Вейерштрасса к степенным рядам.
Теорема Тейлора.
Неравенство Копти для коэффициентов степенного ряда.
Теорема Лиувилля.
Свойство единственности аналитических функций (доказать первую часть).
Свойство единственности аналитических функций (доказать вторую часть).
Нулианалитических функций.
Принцип максимума модуля,
Ряд Лорана и его область сходимости.
Теорема Лорана.
Классификацияизолированных особых точек однозначной аналитический функции.
Устранимая особая точка.
Полюс.
Связь между нулём и полюсом.
Разложение аналитической функции в ряд Лорана. В окрестности бесконечно удалённой точки.
Теорема Сохоцкого-Вейерштрасса.
Вычет. Основная теорема о вычетах.
Вычисление вычета относительно простого полюса.
Вычисление вычета относительно кратного полюса.
Вычетотносительно бесконечно удалённой точки.
Вычисление интегралов вида .
Вычисление интегралов вида
.Лемма Жордана.
Логарифмический вычет.
Принцип Аргумента.
Теорема Руше.
Теорема Гурвица.
Целые функции.
Разложение целой функции в произведение.
Мероморфные функции.
Разложение Миттаг-Леффлера.