66. Вычисление вычетов относительно простого полюса.

1. Пусть – простой полюс первого порядка функции f(z). Тогда Выч[f(z), ]= .

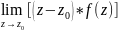2. Пусть – простой полюс первого порядка функции f(z)= , где 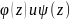- аналитичны в точке , причем 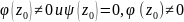. Тогда Выч[f(z), ]= .

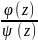67. Вычисление вычетов относительно кратного полюса.

Пусть – полюс m - го порядка функции f(z). Тогда Выч[f(z), ]= .

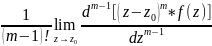68. Вычет относительно бесконечно удаленной точки.

Пусть z₀= бесконечно удаленная точка является изолируемой особой точкой функции f(z). Обозначим через Г произвольный кусочно гладкий замкнутый контур, целиком лежащий в окрестности z= аналитической функции f(z) и содержащая внутри себя нулевую точку.

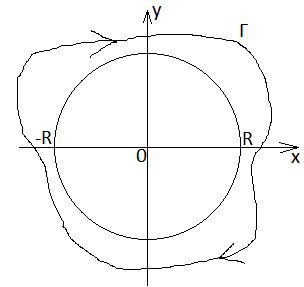
Опр: Вычетом функции f(z) относительно функции z= называется значение интеграла

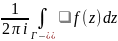и обозначим

Выч[f(z), ]

Оказывается, что

Выч[f(z), ]= -С_-1.

Выч[f(z), ]= =-С_-1.

Теорема:(о полной сумме вычета): f(z) – аналитическая во всей расширенной комплексной плоскости за исключением конечного числа изолированных особых точек z_k, k=1,2,…,N включая и точку z= (z₁= ), тогда

69. Вычисление интегралов вида .

R(u,v) – действительная рациональная функция двух действительных переменных u и v . Причем функция R(cos , sin ) непрерывна на отрезке 0≤ ≤2π.

70. Вычисление интегралов вида .

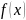– рациональная функция (многочлен поделенный на многочлен)

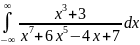
Теорема: Пусть рациональная функция 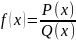, (P(x),Q(x) многочлен) не имеет полюсов на действительной оси, причем степень n многочлена Q(x) по крайней мере на 2 единицы превышает степень m многочлена P(x), т.е.

n-m≥2.

Тогда 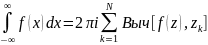, где всякие z_k – различные полюсы f(z), расположенные в верхней полуплоскости (Imz>0) т.е. Imz_k>0.

71. Лемма Жордана.

Лемма: Пусть функция f(z) – аналитическая в замкнутой верхней полуплоскости

Imz≥0 за исключением конечного числа особых точек z₁,z_2,…,z_N расположенных в открытой верхней полуплоскости. Если при этом в замкнутой верхней полуплоскости.

(Imz≥0), f(z) 0 при z→ , то для справедлива формула

Отметим, что формула (1) может быть записана в виде:

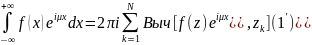
Замечание:Если функция четная, то формула (1) принимает вид:

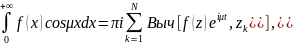
Если – нечетная, то

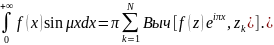
72. Логарифмический вычет

Пусть ф-ция f(z) явл. аналитической как внутри кусочно-гладкого замкнутого контура Г, так и на сомом контуре Г, за исключением.быть может, конечного числа полюсов располо-ных внутри Г. Предположим ещё, что f(z) 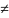0.

Обазначим через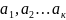 нули ф-ции f(z) внутри Г,а через 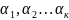- порядки этих нулей. Через 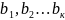- полюсы f(z) в нутрии Г, а через 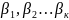порядки полюсов.

Тогда для любого 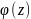ана-ской внутри Г и на Г имеет место равенство

Опр. Интеграл 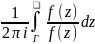наз. логари-ским вычетом ф-ции f(z) относительно контура Г.

Теорема. Лога-ский вычет ф-ции f(z), относительно замкнутого контура Г равен разности между числом нулей и числом полюсов ф-ции f(z) внутри Г, причём каждый нуль и каждый полюс считается столько раз, какова его кратность.

73. Принцип аргумента

Лого-ский вычет имеет достаточно простой смысл. Чтобы раскрыть его представим в следующём виде интеграл

Принцип аргумента:

Разность между коли-ством нулей и коли-ством полюсов ф-ции f(z) заключённых внутри замкнут. кривой Г равна изменению Arg(f(z)) при обходе точкой z контура Г в положительном направлении, делённого на 2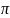 i.

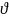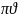Отметим геометрическую интерпретацию аргумента. Обозначим через кол-во полных оборотов вокруг ночала координат, которые совершает точка w=f(z) при обходе точкой z замкнутой кривой Г в положительном направлении. Тогда для изменения Arg(f(z)) получаем величину 2 . Отсюда вытекает геометрическая формули-ка принципа аргумента:

разность между числом нулей и числом полюсов ф-ции f(z) внутри Г, равна числу полных оборотов, которые совершает точка w=f(z) вокруг начала координат, когда точка z описывает контур Г в положительном направлении N-P= .