62. Связь между нулем и полюсом.

Теорема: Если т. - есть нуль порядка 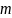для ф-ции (или полюс порядка ), то для ф-ции 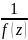будет полюсом порядка (нулем порядка , если считать ).

63. Разложение аналитич. Ф-ции в ряд Лорана в окрес-ти бесконечно удаленной точки (б.У.Т.).

Пусть – аналитична в некоторой окружности б.у.т. . Положим, 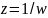, тогда (1)

будет определена и аналитична в кольце , в некотор. проколотой окрес-ти . Сл-но в окрес-ти б.у.т. пл-ти соотв. окрес-ть нулевой т. пл-ти 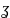. Причем в соотв. точках и функции и принимают равные значения. Поэтому естественно называть б.у.т. существенно о.т. полюсом порядка или устран.о.т. функции в зависимости от того будет ли нулевая точка для функции сущ.о.т. полюсом порядка или устранимой особенностью.

Чтобы получить разложение Лорана для ф-ции в окрес-ти нулевой точки

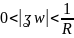, , (2)

т.к. 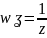, то в силу (1) имеем:

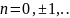, , где , (3)

Соотношение (3) наз. разложением в ряд Лорана в окрес-ти т. .

Опр. Если в разложении (3)

а) нет членов с положит. степенями , то б.у.т. называют у.о.т.

б) есть лишь конечное число членов с положит. степенями , то б.у.т называют полюсом ф-ции .

в) есть бесконечно много членов с положит. степенями , то б.у.т. называется существенной .

В соответствии с этим главной частью разложения Лорана в окрес-ти б.у.т. называется совокупность членов с положит. степенями, а правильной частью - совокупность членов с неположит. степенями .

64. Теорема Сохоцкого-Вейерштрасса.

Теорема С-В: Любое комплексное число А конечное или бесконечное, последовательность - сходящееся к существенной особой т. ф-ции (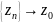 ), такая что .

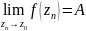Замечание: Из теоремы С-В следует, что если т. - сущ.о.т. ф-ции , то не существует.

65. Вычет. Основная теорема о вычетах.

Пусть – изолированная особая точка, тогда найдется проколотая 0< <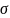 окрестность этой точки, в которой функция f(z) является аналитической. И пусть Г есть кусочно-гладкий замкнутый контур, целиком лежащий в этой окрестности и содержащий точку .

Тогда значение интеграла будет отличаться от нуля. Это значение как следует из интегральной теоремы Коши для составного контура не зависит от формы Г.

Вычислим этот интеграл.

Разложим в ряд Лорана в кольце 0< > :f(z)=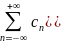 , 0< > (1)

Этот ряд сходится равномерно на линии Г. Поскольку

=

Интегрируя (1) почленно вдоль линии Г получим

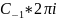= (2)

Значение интеграла 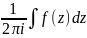называется вычетом функции относительно ее изолированной особой точки и обозначается Выч[f(z), ].

Из (2) имеем Выч[f(z), ]= =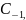 т.е. вычет функции относительно изолированной особой точки равен коэффициенту при первой отрицательной степени ряда Лорана (1).

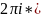= Выч[f(z), ]

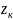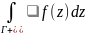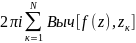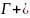Теорема: пусть - аналитическая функция всюду в замкнутой области G, за исключением конечного числа ИОТ , к=1,2,3...,N, лежащих внутри области G. Тогда = , где представляет собой полную границу области G, проходимую в положительном направлении.