55. Нули аналитических функций

Опр. Нулем функции f(z) аналитической в некоторой области G будем называть всякую точку этой области, в которой имеет место равенство f( )=0.

Опр. Натуральное число к называется порядком или кратностью 0 функции f(z), при к=1 называется простым нулем функции, а при к >1 – кратным.

Согласно определению простой нуль характеризуется тем, что f( )=0, а производная не равна 0.

А для кратного нуля только к-ая производная не равна нулю.

56. Принцип максимума модуля.

Теорема. Модуль функции f(z) тождественно не равный const и аналитический в некоторой области G не может иметь максимума ни в одной точке этой области.

57. Ряд Лорана и его область сходимости

Рассмотрим ряд вида (1).

Где - фиксированная точка комплексной плоскости, а - некоторые комплексные числа, а суммирование ведется как по положительным, так и по отрицательным значениям индекса.

Ряд (1) наз. рядом Лорана.

Это ряд рассматривается как сумма двух рядов

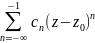и и рассматривается как сходящийся если сходятся оба этих ряда.

Областью сходимости ряда Лорана является общая часть области сход. Суммы рядов.

Область сходимости круговое кольцо , если .

Если же , то ряд Лорана нигде не сходится к какой либо функции.

58. Теорема Лорана

Теорема. Функция f(z) аналитическая в круговом кольце однозначно представляется в этом кольце сходящимся рядом Лорана.

59. Классификация изолированных особ. Точек однознач. Аналитической ф-ции.

Опр. Точка -наз. изолированной особой точкой однозначной ф-ци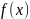и , если окрестность этой точки, в которой ф-ция аналитична всюду, кроме самой т.

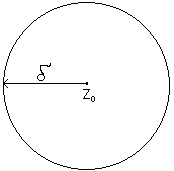
Пусть - есть изолированная особая точка ф-ции , тогда найдется , такая что в кольце 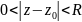будет аналит. В силу теоремы Лорана ф-ция в этом кольце может быть разложена в ряд Лорана:

, . (1)

При этом возможны 3 случая:

1)Разложение (1) не содержит членов с отрицательными степенями разности , в этом случае называется устранимой особой т. ф-ции .

2)Разложение (1) содержит лишь конечное число членов с отрицательными степенями разности , в этом случае называется полюсом.

3) Разложение (1) содержит бесконечное число членов с отрицательными степенями разности ,в этом случае называется существенной особой точкой.

60. Устранимая особая точка.

Теорема 1: Если т. - есть у.о.т. аналитической ф-ции , то конечный предел

Замечание: Из существования конечного предела в частности следует, что в некоторой окрестности у.о.т. функция ограничена по модулю.

Теорема 2: Если ф-ция аналитическая в круговом кольце , ограничена в этом кольце по модулю, то изолированная особая точка ф-ции является у.о.т. этой функции.

61. Полюс.

Теорема: Если т. - есть полюс аналитической ф-ции , то

Д-во: Пусть - полюс ф-ции аналитической в кольце . В этом случае разложение ф-ции в ряд Лорана в кольце будет иметь вид:

,

где (1)

Если , то полюс - называется простым,

Если , то полюс - называется кратным,

.
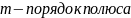