
- •1.Комплексные числа и действия над ними
- •2. Свойства модуля и аргумента
- •3. Последовательность комплексных чисел.
- •4. Бесконечность и стереографическая проекция.
- •5. Множества точек на плоскости.
- •6. Понятие фкп. Предел и непрерывность фкп.
- •7. Дифференцируемость фкп.
- •8. Необходимые и достаточные условия дифференцируемости (доказать необходимость)
- •9. Необходимые и достаточные условия дифференцируемости (доказать достаточность).
- •10. Гармонические функции.
- •11. Геометрический смысл аргумента производной.
- •12. Геометрический смысл модуля производной.
- •13. Понятиео конформных отображениях.
- •14. Линейная функция.
- •15. Отображение .
- •16. Дробно-линейная функция.
- •17. Конформность дробно-линейной функции.
- •18. Параметры и инвариант дробно-линейного отображения.
- •19. Отображения областей, ограниченных прямыми или
- •20. Круговое свойство дробно-линейной функции.
- •21. Свойство симметрии дробно-линейной функции.
- •26. Показательная функция.
- •27. Логарифмическая функция.
- •28. Общая степенная функция.
- •29. Функция Жуковского.
- •30. Тригонометрическая функция.
- •31. Одназначные ветви многозначной функций .
- •32. Поверхность Римана .
- •33. Однозначные ветви многозначной функции и ее поверхность Римана.
- •34. Интеграл от фкп и его свойства.
- •35. Сведение вычисления интеграла от фкп к вычислению обыкновенного интеграла.
- •36. Интегральная теорема Коши для простого контура.
- •37. Интегральная теорема Коши для составного контура.
- •38. Неопределенный интеграл в комплексной области.
- •39. Интегральная формула Коши.
- •40. Интеграл типа Коши.
- •41. Бесконечная дифференцируемость аналитической функции.
- •42. Обращение интегральной теоремы.
- •43. Числовые ряды.
- •44. Функциональные ряды.
- •45.Степенные ряды. Теорема Абеля.
- •46.Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать первую часть).
- •47. Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать вторую часть).
- •48. Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать третью часть).
- •49. Приложение теоремы Вейерштрасса к степенным рядам.
- •50. Теорема Тейлора.
- •51. Неравенство Коши для коэффициентов степенного ряда.
- •52. Теорема Лиувилля.
- •53. Свойства единственности аналитических функций.
- •54. Свойство единственности аналитических функций (доказать вторую часть)
- •55. Нули аналитических функций
- •56. Принцип максимума модуля.
- •57. Ряд Лорана и его область сходимости
- •58. Теорема Лорана
- •59. Классификация изолированных особ. Точек однознач. Аналитической ф-ции.
- •60. Устранимая особая точка.
- •61. Полюс.
- •62. Связь между нулем и полюсом.
- •63. Разложение аналитич. Ф-ции в ряд Лорана в окрес-ти бесконечно удаленной точки (б.У.Т.).
- •64. Теорема Сохоцкого-Вейерштрасса.
- •65. Вычет. Основная теорема о вычетах.
- •66. Вычисление вычетов относительно простого полюса.
- •67. Вычисление вычетов относительно кратного полюса.
- •68. Вычет относительно бесконечно удаленной точки.
- •69. Вычисление интегралов вида .
- •70. Вычисление интегралов вида .
- •71. Лемма Жордана.
- •72. Логарифмический вычет
- •73. Принцип аргумента
- •74. Теорема Руше
- •75. Теорема Гурвица
- •76. Целые функции
- •77. Разложение целой функции в произведение.
- •78. Мероморфные функций.
- •79. Разложение Миттаг-Леффлера.
50. Теорема Тейлора.
Теорема. Функция f(z) аналитическая внутри некоторого круга однозначно разлагается в этом круге в степенной ряд.
Замечание: Если функция f(z) является аналитической во всей комплексной плоскости C, то пологая =0 получим, что
f(z)=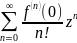 ,
|z|<
,
|z|<
Вычислим
производные различных порядков от
элементарных функций
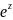 ,
,
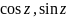 аналитические во всей комплексной
плоскости, можно легко получить для них
следующие сходящие во всей плоскости
разложения:
аналитические во всей комплексной
плоскости, можно легко получить для них
следующие сходящие во всей плоскости
разложения:
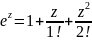 +…+
+…+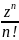 =
=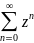 ,
|z|<
,
|z|<
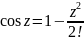 +
+ -
-
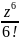 +…+
+…+ +
+…=
+
+…= ,
|z|<
,
|z|<
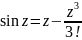 +
+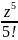 -
…+
-
…+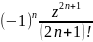 +
+…=
+
+…= ,
|z|<
,
|z|<
51. Неравенство Коши для коэффициентов степенного ряда.
Теорема:
Если степенной ряд f(z)=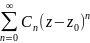 сходится в круге |
сходится в круге | |<R
и изобр. в нем функцию f(z),
модуль которой все время меньше М, то
есть |f(z)|<M=const,
то имеет место неравенство |
|<R
и изобр. в нем функцию f(z),
модуль которой все время меньше М, то
есть |f(z)|<M=const,
то имеет место неравенство |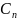 |≤
|≤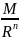 , n=0,1,2,…
, n=0,1,2,…
Доказательство: Воспользуемся интегральным выражением для коэффициентов степенного ряда
=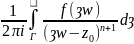 , n=0,1,2,…. ,
, n=0,1,2,…. ,
где интегрирование ведется по окружности
Г:|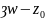 |=
<R
|=
<R
Оценивая | | находим
|
|<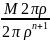 , |
|<
, |
|<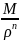 , n=0,1,….
, n=0,1,….
Так
как последнее неравенство справедливо
при
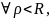 то путем придельного перехода при
то путем придельного перехода при
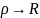 окончательно находим |
|≤
, n=0,1,2,…
.
окончательно находим |
|≤
, n=0,1,2,…
.
52. Теорема Лиувилля.
Теорема: Если функция f(z) является аналитической во всей комплексной плоскости и ограничена в ней по модулю, то она есть тождественная постоянная.
Доказательство:
Действительно, в этом случаи разложение
f(z)=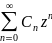 имеет место во всякой точки z
плоскости Z.
Пользуясь неравенствами Коши для
коэффициентов степенного ряда имеем,
что |
|≤
, n=0,1,2,…
М=const,
а R-
сколь угодно большое может быть.
имеет место во всякой точки z
плоскости Z.
Пользуясь неравенствами Коши для
коэффициентов степенного ряда имеем,
что |
|≤
, n=0,1,2,…
М=const,
а R-
сколь угодно большое может быть.
Следовательно
имеем, что
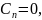 при
n≥1
при
n≥1
f(z)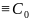 =const.
=const.
В качестве простого примера приложения теоремы Лиувилля приведем теорему высшей алгебры.
Теорема:
Всякий
многочлен P(z)=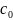 +
+ +
+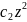 +…+
+…+ ,
(n≥1,
,
(n≥1, )
)
Имеет по крайней мере один корень(ноль).
53. Свойства единственности аналитических функций.
Теорема:
Если две функции f(z)
и
(z)
аналитические в некоторой области G
имеют равные значения на бесконечном
множестве точек E
этой области. E G,
причем, множество E
имеет по крайней мере одну придельную
точку, лежащую внутри области G,
то эти функции равны между собой всюду
в области G,
то есть f(z)
G,
причем, множество E
имеет по крайней мере одну придельную
точку, лежащую внутри области G,
то эти функции равны между собой всюду
в области G,
то есть f(z)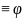 (z)
для
z
G.
(z)
для
z
G.
54. Свойство единственности аналитических функций (доказать вторую часть)
Теорема:
Если 2 функции
 аналитические в некоторой области G
имеют равные значения на бесконечном
множестве точек E
аналитические в некоторой области G
имеют равные значения на бесконечном
множестве точек E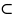 G,
причем мн-во E
имеет по крайней мере хотя бы одну
предельную точку, локальную в области
G,
то эти функции равны между собой всюду
в этой области.
G,
причем мн-во E
имеет по крайней мере хотя бы одну
предельную точку, локальную в области
G,
то эти функции равны между собой всюду
в этой области.
Д-во:
Пусть
область G
произвольной формы и пусть точка
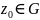 является предельной точкой множества
Е. Покажем, что наши функции имеют равные
значения в произвольной точке z
из G.
Для этого соединим эти точки произвольной
линией Г, лежащей в этой области. Обозначим
через d>0
расстояние от линии до границы области.
Очевидно, что тогда круг радиуса d/2
будет целиком принадлежать нашей
области. Заставим центр круга радиусам
d/2
непрерывно двигаться по линии Г от точки
к точке. Тогда наши функции должны
совпадать между собой внутри движущегося
круга. Функции будут равны.
является предельной точкой множества
Е. Покажем, что наши функции имеют равные
значения в произвольной точке z
из G.
Для этого соединим эти точки произвольной
линией Г, лежащей в этой области. Обозначим
через d>0
расстояние от линии до границы области.
Очевидно, что тогда круг радиуса d/2
будет целиком принадлежать нашей
области. Заставим центр круга радиусам
d/2
непрерывно двигаться по линии Г от точки
к точке. Тогда наши функции должны
совпадать между собой внутри движущегося
круга. Функции будут равны.
