44. Функциональные ряды.

Рассмотрим функциональный ряд 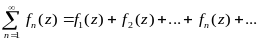(1) все члены которого есть однозначные функции комплексного переменного , определённого в некоторой области . Предположим, что этот ряд сходится в каждой точке области , в этом случае сумма ряда будет представлять собой однозначную функцию в области .

Определение:Ряд (1) наз равномерно сходящимся в области к функци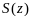и , если , такое , что неравенство выполняется сразу

( ).

Т.к. приведённое определение равномерной сходимости дословно совпадает с соответствующим определением из мат анна, то для равномерно сходящихся рядов в комплексной области остаются справедливыми следующие утверждения.

Теорема1: Если все - непрерывны в области , а ряд сходится равномерно в этой области, то его сумма непрерывна в области .

Теорема2(Признак равномерной сходимости Вейерштрасса):

Если все для и числовой ряд сходится, то ряд сходится абсолютно и равномерно в области .

Теорема 3:Если функции непрерывны на линии и ряд 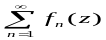сходится равномерно на , то данный ряд можно почленно интегрировать, т.е. .

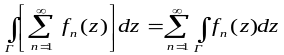45.Степенные ряды. Теорема Абеля.

Степенным рядом наз. ряд вида: где 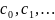- фиксированные комплексные числа, – комплексная переменная, – центр ряда (фиксированное комплексное число). Заменим на : (1)

Теорема1 (Абеля): Если степенной ряд (1) сходится в точке , то он сходится и притом абсолютно во всех точках : .

Доказательство:

Согласно условию теоремы числов. ряд - сходится, в силу необходимого признака сходимости , отсюда следует, что , тогда при будем иметь: , где , но ряд есть сумма бесконечно убывающей геометрической прогрессии, поэтому ряд - сходится при , а это означает, что ряд - сходится абсолютно, при . ⊠

В терминах геометрии теорему Абеля можно сформулировать: если степенной ряд (1) сходится в точке , то он сходится абсолютно во всякой точке лежащей внутри окружности с центром в начале коорд. и проходящей через точку .

Следствие: Если степенной ряд (1) расходится в точке , то он расходится во всех точках для которых .

Теорема 1: Для любого степенного ряда 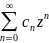существует круг конечного или бесконечного радиуса внутри которого ряд абсолютно сходится, а вне круга – расходится. Такой круг наз. кругом сходимости, а его радиус - радиусом сходимости данного ряда.

Поведение ряда на окружности круга сходимости остаётся неопределённым, т.к. ряд в круге сходимости сходится абсолютно, то для определения этого круга можно применять признак Коши, Даламбера. Радиус сходимости можно определять и с помощью:

Теорема 2: Ряда радиус сходимости определяется по формуле , где ( = последовательности { } ), т.е. наибольший из частичных пределов этой последовательности. Формула: наз. формулой Коши – Адамара.

46.Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать первую часть).

Теорема: Пусть функции являются аналитическими в некоторой области , а ряд 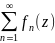(1) сходится равномерно во всякой замкнутой подобласти функции , тогда:

1. Функц. - явл. аналитической в обл.

2. 

3. Ряд - сход.равномерно во всякой подобл.

Доказательство:

1)В силу равномерной сходимости (1) его сумма есть функция непрерывная всюду в обл. .

Пусть – произвольная точка обл. . Покажем, что в точке функция имеет конечную производную. Окружим точку кусочно-гладким замкнутым контуром так, чтобы он целиком лежал в обл. . Данный ряд (1) по условию теоремы будет равномерно сходится на контуре и в точке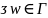 будет справедливо равенство: 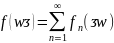(2).

Обозначим через расстояние от точки до контура , тогда имеем: , поэтому функция – будет ограниченной по модулю на контуре , т.к. 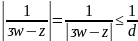умножим все члены равенства (2) на , полученный ряд – будет равномерно сходится на контуре . Такой ряд можно почленно интегрировать вдоль , интегрируя вдоль линии , а затем разделив почленно на 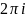: 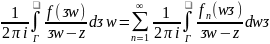(3) , т.к. функции есть аналитические как внутри так и на , то пользуясь интегральной формулой Коши перепишем (3) в виде: , отсюда , т.е. функция изображается интегралом типа Коши во всех внутренних точках контура , поэтому она во всех внутренних точках контура имеет конечную производную, а т.к. – производная точка обл. , то следует, что функция – аналитическая в обл. .