
- •1.Комплексные числа и действия над ними
- •2. Свойства модуля и аргумента
- •3. Последовательность комплексных чисел.
- •4. Бесконечность и стереографическая проекция.
- •5. Множества точек на плоскости.
- •6. Понятие фкп. Предел и непрерывность фкп.
- •7. Дифференцируемость фкп.
- •8. Необходимые и достаточные условия дифференцируемости (доказать необходимость)
- •9. Необходимые и достаточные условия дифференцируемости (доказать достаточность).
- •10. Гармонические функции.
- •11. Геометрический смысл аргумента производной.
- •12. Геометрический смысл модуля производной.
- •13. Понятиео конформных отображениях.
- •14. Линейная функция.
- •15. Отображение .
- •16. Дробно-линейная функция.
- •17. Конформность дробно-линейной функции.
- •18. Параметры и инвариант дробно-линейного отображения.
- •19. Отображения областей, ограниченных прямыми или
- •20. Круговое свойство дробно-линейной функции.
- •21. Свойство симметрии дробно-линейной функции.
- •26. Показательная функция.
- •27. Логарифмическая функция.
- •28. Общая степенная функция.
- •29. Функция Жуковского.
- •30. Тригонометрическая функция.
- •31. Одназначные ветви многозначной функций .
- •32. Поверхность Римана .
- •33. Однозначные ветви многозначной функции и ее поверхность Римана.
- •34. Интеграл от фкп и его свойства.
- •35. Сведение вычисления интеграла от фкп к вычислению обыкновенного интеграла.
- •36. Интегральная теорема Коши для простого контура.
- •37. Интегральная теорема Коши для составного контура.
- •38. Неопределенный интеграл в комплексной области.
- •39. Интегральная формула Коши.
- •40. Интеграл типа Коши.
- •41. Бесконечная дифференцируемость аналитической функции.
- •42. Обращение интегральной теоремы.
- •43. Числовые ряды.
- •44. Функциональные ряды.
- •45.Степенные ряды. Теорема Абеля.
- •46.Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать первую часть).
- •47. Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать вторую часть).
- •48. Теорема Вейерштрасса о равномерно сходящихся рядах аналитических функций (доказать третью часть).
- •49. Приложение теоремы Вейерштрасса к степенным рядам.
- •50. Теорема Тейлора.
- •51. Неравенство Коши для коэффициентов степенного ряда.
- •52. Теорема Лиувилля.
- •53. Свойства единственности аналитических функций.
- •54. Свойство единственности аналитических функций (доказать вторую часть)
- •55. Нули аналитических функций
- •56. Принцип максимума модуля.
- •57. Ряд Лорана и его область сходимости
- •58. Теорема Лорана
- •59. Классификация изолированных особ. Точек однознач. Аналитической ф-ции.
- •60. Устранимая особая точка.
- •61. Полюс.
- •62. Связь между нулем и полюсом.
- •63. Разложение аналитич. Ф-ции в ряд Лорана в окрес-ти бесконечно удаленной точки (б.У.Т.).
- •64. Теорема Сохоцкого-Вейерштрасса.
- •65. Вычет. Основная теорема о вычетах.
- •66. Вычисление вычетов относительно простого полюса.
- •67. Вычисление вычетов относительно кратного полюса.
- •68. Вычет относительно бесконечно удаленной точки.
- •69. Вычисление интегралов вида .
- •70. Вычисление интегралов вида .
- •71. Лемма Жордана.
- •72. Логарифмический вычет
- •73. Принцип аргумента
- •74. Теорема Руше
- •75. Теорема Гурвица
- •76. Целые функции
- •77. Разложение целой функции в произведение.
- •78. Мероморфные функций.
- •79. Разложение Миттаг-Леффлера.
38. Неопределенный интеграл в комплексной области.
Из интегральной теоремы Коши вытекает следующее важное
Свойство:
если f(z)
аналитическая в односвязной области
G,
то значения интеграла
 взятого вдоль произвольной кусочно-гладкой
кривой Г принадлежит области G
не зависит от линии Г, а определяется
лишь положениями начальной и конечной
точками этой линии.
взятого вдоль произвольной кусочно-гладкой
кривой Г принадлежит области G
не зависит от линии Г, а определяется
лишь положениями начальной и конечной
точками этой линии.
Теорема:
Функция
f(z)
непрерывна в односвязной области G
для которой интегралы вдоль любых
кусочно-гладких линий принадлежащих
области G
зависят только от начальной и конечной
точек кривых. Тогда функция F(z)=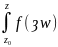 dw
является аналитической в области G,
причем
dw
является аналитической в области G,
причем
 (z)=f(z)
(z)=f(z)
Определение:
Ф(z)
– аналитическая в некоторой области G
называется неопределенным интегралом
или первообразной от функции f(z)
в области G,
если Ф`(z)=f(z)
для
 z
z G.
G.
Очевидно,
что если f(z)
удовлетворяет условием сформулированной
выше теоремы, то функция Ф(z)= dw
есть первообразная от f(z)
в области G.
dw
есть первообразная от f(z)
в области G.
Можно показать, что любая первообразная от f(z) может быть записана в виде Ф(z)= dw+С, где С-комплексная постоянная. Пологая в этой формуле z= , получим, что Ф( )=С, тогда
dw= Ф(z)-Ф( ).
Полученный результат по формуле совпадает с известной формулой Ньютона-Лейбница и сводит вычисление интеграла от аналитической функции f(z) к исканию какой-либо ее первообразной.
Итак, ограниченая функциями аналитическими в односвязной области мы видим, что подобна обыкновенным интегралом интегрирование по комплекснай переменной можно рассматривать с двух точек зрения:
Как процесс суммирования.
Как действие обратное дифференцированию.
В заключении отметим, что оказываются справедливыми и все приемы вычисления интегралов , основанные на формуле Ньютона-Лейбница. Например: интегрирование по частям, замена переменной.
39. Интегральная формула Коши.
Пусть G есть односвязная область ограниченная произвольным кусочно-гладким контуром Г и пусть f(z) есть функция аналитическая в замкнутой области G, то есть аналитическая как внутри области G так и на ее границе Г.
Выведем
интегральную формулу Коши f(z)= w,
где z-любая
точка внутри Г, а интегрирование по
контуру Г ведется в положительном
направлении.
w,
где z-любая
точка внутри Г, а интегрирование по
контуру Г ведется в положительном
направлении.
Эта формула выражает значение аналитической функции внутри замкнутой кривой через значение той же функции на этой кривой.
Для доказательства рассмотрим вспомогательную функцию
(w)=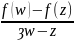 (z-любая
точка, но фиксированная)
(z-любая
точка, но фиксированная)
Эта функция (w) является аналитической во всех точках w G кроме точки w=z.
Опишем из точки z как центра окружность произвольного радиуса целиком лежащую в области G. Тогда функция (w) будет аналитическая во всех точках, лежащих между контурами Г и включая и сами контуры. Следовательно, на основании интегральной теоремы Коши для составного контура будем иметь
 dw=
dw= dw
(1)
dw
(1)
Равенство
(1) показывает, что значения
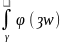 dw
не зависит от радиуса
вспомогательной окружности
так как он равен постоянному числу
dw.
dw
не зависит от радиуса
вспомогательной окружности
так как он равен постоянному числу
dw.
Заметим
далее, что функция
 к определенному приделу когда w
к определенному приделу когда w z.
Действительно,
z.
Действительно,
 =
= =f’(z)
так как f(z)
аналитическая в G.
Следовательно, если f’(z)
принять за значения функции
=f’(z)
так как f(z)
аналитическая в G.
Следовательно, если f’(z)
принять за значения функции
 в
точке w=z,
то функция
в
точке w=z,
то функция
 станет непрерывной всюду в замкнутой
областиG
, поэтому |
|<M=const
для всех w
G.
станет непрерывной всюду в замкнутой
областиG
, поэтому |
|<M=const
для всех w
G.
| dw|<M*2
dw|<M*2 так как
dw
есть постоянное число, а
может принимать сколь угодно малое
значения, то интеграл равен нулю.
так как
dw
есть постоянное число, а
может принимать сколь угодно малое
значения, то интеграл равен нулю.
Перепишем
(1) в виде
dw=0,
то есть
 dw=0.
Отсюда,
dw=0.
Отсюда,
 dw=
dw=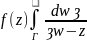 ,
, dz=f(z)2
dz=f(z)2 ,
f(z)=
,
f(z)= .
.
