1.Комплексные числа и действия над ними

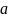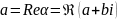Как известно каждое комплексное число в алгебраической форме имеет вид и действительные числа, а мнимая единица определяемая соотношением . Число называется действительной частью комплексного числа и обозначается , и обозначается

Действительные числа естественно составляют часть комплексных чисел, а именно каждое действительное число есть такое комплексное число .

По определению два комплексных числа считаются равными друг друга, тогда и только тогда, когда у них соответственно равны действительные и мнимые части, другими словами <=> . Сложение, вычитание и умножение комплексных чисел производят по обычным правилам алгебры многочлена, заменяя каждый раз на . При делений частное записывается в виде дроби, а затем числитель и знаменатель умножают на число сопряженным знаменателю. Комплексное число . Геометрическая интерпретация комплексных чисел

Для геометрического изображения комплексных чисел задают на плоскости прямоугольную декартовую систему координат и каждую точка рассматривают как образ числа . Это условие устанавливает взаимно-однозначное соответствие между множествами всех комплексных чисел. При этом множество всех действительных чисел изображается на оси , которая поэтому и называется действительной осью, а множество всех чисто мнимых чисел – на оси ординат наз. мнимой осью. Плоскости точки, которой изображают комплексные числа наз. комплексной плоскостью. Для геометрического представления комплексного числа 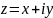кроме точки используется ещё и вектор с проекциями и на координатные оси.

Пусть есть полярные координаты точки М. следовательно т.е тригонометрическая форма комплексного числа Число модуль комплексного числа и обозначается 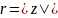очевидн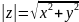о . Число есть угол между положительными направлением оси и вектором наз аргументом и обозначается . Очевидно, что модуль определяется однозначно. Аргумент определении с точностью до целого кратного . Эти значения определить из системы уравнения . Значения аргумента заключенное в границах ( ) называются главными значениями аргумента и обозначают символом . Таким образом, . Очевидно, что не имеет смысла говорить об аргументе нуля так как в этом случае вектор изображающее число вырождается в точку. Ясно, что . Не трудно заменить, что два комплексных числа записанных в тригонометрической форме равны друг другу тогда и только когда модули равны, а аргументы или равны или отличаются на число кратное , т.е.

Воспользовавшись формулой Эйлера получим, что . показательная форма комплексного числа. Комплексные числа не сравниваются друг с другом. Однако сравнимы модули комплексных чисел.

2. Свойства модуля и аргумента

Док-во. Пусть

Легко распространяются на случай произвольного конечного числа комплексных сомножителя. Для такого произведения имеют место равенства

.

Отсюда если все множители равны между собой и равны , то легко заметить, что (2)

Равенство (2) выражает формулу Муавра.

Рассмотрим операцию извлечения корня для комплексного числа . Решим уравнение

Множество решений это уравнения обозначим символом и назовём его корнем й степени из комплексного числа .

Из формулы Муавра (3) легко получается формула для извлечения корня

есть арифметическое значения корня, a одно из значений аргумента w. Если к придавать другие значения, то значения корня начнут повторяться. Легко убедиться, что все значений корня геометрически изображаются точками вершинах правильного ка с центром в начале координат.

По определению частного имеем . применяем свойство 1.

Для любых комплексных чисел справедливо и

равен расстоянию между точками и .

Свойство 3 и 4 легко проверяются геометрически.