5. Теорема Сложения вероятностей совместных событий.

Суммой 2-х совместных событий называют событие, состоящее в появлении либо события A, либо события B, либо обоих сразу. 

Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p(A+B)=p(A)+p(B)−p(AB) 

Доказательство:

A+B=AB+AB+AB (сумма несовместных пар)

Тогда p(A+B)=p(AB)+p(AB)+p(AB)

Событие A=AB+AB,

Событие B=AB+AB

p(A+B)=p(A)−p(AB)+p(B)−p(AB)+p(AB)=p(A)+p(B)−p(AB) 

Замечание: в этой теореме может существовать 2 различные ситуации.

p(A+B)=p(A)+p(B)−p(A)p(B),  где A и B - независимые;

p(A+B)=p(A)+p(B)−p(A)p(B∖A),  где A и B - зависимые;

6. Формула полной вероятности. Вероятность гипотез. Формула Бейеса.

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Формулировка

Пусть дано вероятностное пространство  , и полная группа попарно несовместных событий  , таких что            . Пусть   — интересующее нас событие. Тогда

.

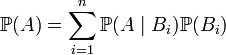Замечание

Формула полной вероятности также имеет следующую интерпретацию. Пусть   — случайная величина, имеющая распределение

.

Тогда

,

т.е. априорная вероятность события равна среднему его апостериорной вероятности.

Вероятность гипотез. Формула Бейеса.

практически любое утверждение в статистике

рассматривается как гипотеза, то есть некоторое предположение о наличии,

форме, тесноте взаимосвязей.

Предположим, событие Е наступает только при появлении одного из несовместных

событий ,

образующих полную группу. Допустим, в результате испытания событие Е произошло,

то есть достоверным стало одно из событий

или или

или .

Каждое из этих событий рассматривается как гипотетическое и его вероятность как

раз определяется по формуле Байеса.

Предыдущий пример: Известно, что в магазин поставлен стандартный

картофель. Какова вероятность того, что он из четвертой партии.

Таким образом, только в 16-ти случаях из 100 доставленная в магазин

стандартная продукция окажется из четвертой партии.

Применение формулы Байеса позволяет переоценить вероятности гипотез по результатам испытаний, в следствие которых появилось событие Е.

Достоинство формулы Байеса в том, что она может применяться при отсутствии сведений о числе элементарных исходов, достаточно знать вероятности или частности событий.

7. Повторные испытания. Формула Бернулли. Локальная теорема Лапласа

 Повторение испытаний 

Формула Бернулли

 

где   - вероятность появления события A ровно k раз при n независимых испытаниях; p - вероятность появления события A при каждом испытании.

Вероятность того, что при этом событие A:

1) наступит n раз:  ;

 2) не наступит ни разу:  ;

 3) наступит хотя бы один раз:  ;

 4) наступит не более k раз:  ;

 5) наступит не менее k раз:  .

  Локальная теорема Лапласа 

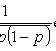
где   - вероятность появления события A ровно k раз при n независимых испытаниях; p - вероятность появления события A при каждом испытании;  .